#4751 医学部受験数Ⅲ分野の解説動画紹介 May 10, 2022 [52. 数学]
大阪市立博物館に勤務しているFB友が、おもしろい数Ⅲ分野の解説動画のURLを貼り付けていたので、クリックしてみました。林俊介という人が大正14年の東大医学部の入試問題の解説をしています。数学から見た解説を一通り終えた後で、「物理現象としてこの関数で近似できるのは...」と飽和関数と物理現象との関係を解説しています。鮮やかな解説ですね、これは高校物理をとれなかったわたしにはとってもありがたい動画です。
博物館の学芸員の人が紹介していたのは「飽和関数と現象の数理モデル」です、難関大学医学部や物理学科を受験したい生徒や好奇心のある人は青字の部分をクリックしてご覧いただきたい。わかりやすい解説です。こういう者を利用できるのだから、根室高校からだって東大理学部物理学科へ現役合格生が出ても不思議じゃないね。いい時代だ、高校生がうらやましい。わたしも勉強させてもらいます。(笑)
「最難関の数学・物理by林俊介」にいままでにアップした数学・物理解説動画の一覧が掲載されているので、見たいものをそこから選んでご覧ください。
<余談:夏目雄平先生のZoom授業>
千葉大名誉教授の夏目雄平先生がご自分の著書の解説をZoomでアップしてくれました。昨年11月ころからだったでしょうかね。新年度の授業の準備用でした。FB友にも視聴できるように配慮してくれたので、拝聴しました。
千葉大の学生へZoom授業の「予行演習」のために意図されたものです。FB友から意見を聞いてそれを本番のZoom授業へ活かす、そういう趣旨でした。本を一冊、章別に解説していただいたので、理系の物理の講義の概要を覗くことができました。文系出身の者にも、物理を学ぶ足がかりを提供してくれたわけです。
感謝 ...m(_ _)m

にほんブログ村
博物館の学芸員の人が紹介していたのは「飽和関数と現象の数理モデル」です、難関大学医学部や物理学科を受験したい生徒や好奇心のある人は青字の部分をクリックしてご覧いただきたい。わかりやすい解説です。こういう者を利用できるのだから、根室高校からだって東大理学部物理学科へ現役合格生が出ても不思議じゃないね。いい時代だ、高校生がうらやましい。わたしも勉強させてもらいます。(笑)
「最難関の数学・物理by林俊介」にいままでにアップした数学・物理解説動画の一覧が掲載されているので、見たいものをそこから選んでご覧ください。
<余談:夏目雄平先生のZoom授業>
千葉大名誉教授の夏目雄平先生がご自分の著書の解説をZoomでアップしてくれました。昨年11月ころからだったでしょうかね。新年度の授業の準備用でした。FB友にも視聴できるように配慮してくれたので、拝聴しました。
千葉大の学生へZoom授業の「予行演習」のために意図されたものです。FB友から意見を聞いてそれを本番のZoom授業へ活かす、そういう趣旨でした。本を一冊、章別に解説していただいたので、理系の物理の講義の概要を覗くことができました。文系出身の者にも、物理を学ぶ足がかりを提供してくれたわけです。
感謝 ...m(_ _)m
にほんブログ村
#4736 数Ⅰと数Aの五段階評価が5だったと喜ぶ生徒 April 8、2020 [52. 数学]
<最終更新情報>4/10午前1時半 余談追記
昨日来た生徒が、数Ⅰと数Aの評価が5だったと笑顔で報告してくれた。授業中や放課後に数学が苦手な生徒によく教えてあげていたし、授業中も先生に協力していたから、認めてくれたのだろう。得点だけの評価ではありません。特設コースのAクラス以外で数学の評定が5は珍しいはず。
部活に一生懸命な生徒でボールを毎日追いかけている。自宅にゴールポストまであるくらい大好きなのだ。中学時代は数学の成績はあまり振るわなかった。本人は自信があるのだが、テストが戻ってくるとチョンボだらけで、本人の自己採点とは数十点の開きがいつもあった。勉強の仕方がわからなかったのだろう。ようやくしっかり点数が採れるようになって半年、点数以上の評価だと思う。性格の良いところが幸いしたのだろう、数学担当の先生に歓迎されているようだ、それはそれでうれしいね。社会人となったときは、人にかわいがられるというのも大事な要素だからだ。
成績が真ん中くらいの生徒が全員こうなってほしいが、なかなかそうはいかぬのが現実です。でも、5人に一人ぐらいはそういう生徒が出現します。もちろん本人が家でも予習方式でしっかり勉強するからです。成長著しい1年間でした。
数ⅠAのなだらかな坂比べると、数ⅡBは勾配のきつい急坂にたとえられます。しっかり勉強を続けてもらいたい。急坂は気を抜くと転げ落ちることがあるよ、そして毎年そういう人が多い。予習方式でしっかり勉強してください。
3月に卒業した生徒は模試の得点が高くていつも全国偏差値が60前後でしたが、学校の定期テストの点数がなぜか取れずに悩んでいました。模試の方が点数が高い生徒なんて他にはいませんからね。でも、最後の半年は、学校の定期テストの点数が大幅にアップして5になったと喜んでいました英検2級にチャレンジするためにメールでの英作文配信の継続を頼まれてます。I・Mさん、同じ大学を受けた3人の受験生の内一人だけ学校推薦で合格できたと言ってましたが、大学の入学式は済んだかな?4年間の勉強修行のスタートですね。技術職だから、正社員で就職できるようにしっかり学んでください。四年間が過ぎるのは速いのです。
<余談:成績は生徒が自らあげる、わたしはちょっとお手伝い>
最後に紹介した生徒は、高校1年生の8月下旬に入塾した生徒です。3歳から幼児英語教室へ通っていました。発音のきれいな生徒でした。一時期、発音矯正指導がとってもきつくて、涙目になりながらやっていたと言ってましたね。しかし、効果は大きかった。高校生になって、その塾の高1数学の授業がなくなりました。模試の成績が学年50番台となって、「Aクラスから落ちてしまう」と慌てて8月24日にきたのです。生徒たちが初めて受ける全国模試である7月のベネッセ模試の結果は8月に生徒に通知されています。全国平均が35点、根室高校普通科の平均点は21-23点くらいです。あいにくと高校数学と英語の両方を教える塾は根室市内には他にはありません。特設コースに居続けるためには選択の余地はなかったわけです。よく来てくれました。(笑)
模試の点数とその順位も特設コースのA組メンバー入れ替えの判断基準でした。11月模試で20番くらいまでアップして、そのままずっと特設コースのクラスでしたね。数学の模試の順位は、いい時は学年5番くらいでした。全国偏差値が60前後で安定してました。
最初の内は共通テストレベルの問題になると、解説を読んでもわからないことだらけ。よく質問してました。模試の過去問を2年分しっかりやるようにしていたので、模試の点数がよかった。それなのに学校の定期テストはサッパリ点数が上がらず、数学担当の先生も首をかしげていました。難易度の高い模試の問題はできるのですが、学校の定期テストの易しい問題ができない。
テストの後で確認すると、基礎的な知識がときどきしっちゃかめっちゃかになっているんです。わけのわからないことをしてしまう。じつは小中の算数や数学の基礎部分に穴がいっぱい開いていました。以前通っていた塾の集団授業が彼女の学力レベルには難易度が高すぎて合わなかったのだろうと思います。理解できない授業を聞いていた。成績上位の生徒に合わせた授業をしてしまうと、中位の生徒には理解できない授業になります。これは学校の授業とは反対です。学校の授業は学力中位の生徒にチューニングした授業になっているので、一部の高学力の生徒はスポイルされてしまっています。自分で難易度の高い問題集を解いていた方が、時間のロスにならなくていい。
個別指導が彼女には合っていました。過去問やってわからない箇所を塾で毎回質問してました。共通テストレベルの難易度の宿題を数学担当の先生がよく出していましたが、ビデオ解説をアップしていて、先生が発行したQRコードをスマホで読み込むとそれを視聴できるのですが、その解説も途中からわからなくなり、塾へもってきて毎回質問して、納得する、そんなことを繰り返していました。個別指導なら共通テストレベルの問題の解説をしながら、小学校算数や中学校の数学で取りこぼした基礎的な知識も整理しながら教えることができます。小学校の算数からやり直す必要はないわけです。生徒の質問に答えながら、こちらから要所要所で質問を生徒に投げたら、どこに穴が開いているのかわかります。それが個別指導のキモなのです。
彼女は質問を繰り返しながら、自分に合ったやり方を見つけてよく勉強したのです。
試行錯誤しながらなんとかやってみる、そして自分に合ったやり方を見つけてしまう。そうやって生徒は成長してしまいます。
塾先生はサポートに回るだけですよ、しっかり成長する生徒自身が偉いのです。毎年こういう生徒が出現するので、塾稼業は愉しい。

にほんブログ村
昨日来た生徒が、数Ⅰと数Aの評価が5だったと笑顔で報告してくれた。授業中や放課後に数学が苦手な生徒によく教えてあげていたし、授業中も先生に協力していたから、認めてくれたのだろう。得点だけの評価ではありません。特設コースのAクラス以外で数学の評定が5は珍しいはず。
部活に一生懸命な生徒でボールを毎日追いかけている。自宅にゴールポストまであるくらい大好きなのだ。中学時代は数学の成績はあまり振るわなかった。本人は自信があるのだが、テストが戻ってくるとチョンボだらけで、本人の自己採点とは数十点の開きがいつもあった。勉強の仕方がわからなかったのだろう。ようやくしっかり点数が採れるようになって半年、点数以上の評価だと思う。性格の良いところが幸いしたのだろう、数学担当の先生に歓迎されているようだ、それはそれでうれしいね。社会人となったときは、人にかわいがられるというのも大事な要素だからだ。
成績が真ん中くらいの生徒が全員こうなってほしいが、なかなかそうはいかぬのが現実です。でも、5人に一人ぐらいはそういう生徒が出現します。もちろん本人が家でも予習方式でしっかり勉強するからです。成長著しい1年間でした。
数ⅠAのなだらかな坂比べると、数ⅡBは勾配のきつい急坂にたとえられます。しっかり勉強を続けてもらいたい。急坂は気を抜くと転げ落ちることがあるよ、そして毎年そういう人が多い。予習方式でしっかり勉強してください。
3月に卒業した生徒は模試の得点が高くていつも全国偏差値が60前後でしたが、学校の定期テストの点数がなぜか取れずに悩んでいました。模試の方が点数が高い生徒なんて他にはいませんからね。でも、最後の半年は、学校の定期テストの点数が大幅にアップして5になったと喜んでいました英検2級にチャレンジするためにメールでの英作文配信の継続を頼まれてます。I・Mさん、同じ大学を受けた3人の受験生の内一人だけ学校推薦で合格できたと言ってましたが、大学の入学式は済んだかな?4年間の勉強修行のスタートですね。技術職だから、正社員で就職できるようにしっかり学んでください。四年間が過ぎるのは速いのです。
<余談:成績は生徒が自らあげる、わたしはちょっとお手伝い>
最後に紹介した生徒は、高校1年生の8月下旬に入塾した生徒です。3歳から幼児英語教室へ通っていました。発音のきれいな生徒でした。一時期、発音矯正指導がとってもきつくて、涙目になりながらやっていたと言ってましたね。しかし、効果は大きかった。高校生になって、その塾の高1数学の授業がなくなりました。模試の成績が学年50番台となって、「Aクラスから落ちてしまう」と慌てて8月24日にきたのです。生徒たちが初めて受ける全国模試である7月のベネッセ模試の結果は8月に生徒に通知されています。全国平均が35点、根室高校普通科の平均点は21-23点くらいです。あいにくと高校数学と英語の両方を教える塾は根室市内には他にはありません。特設コースに居続けるためには選択の余地はなかったわけです。よく来てくれました。(笑)
模試の点数とその順位も特設コースのA組メンバー入れ替えの判断基準でした。11月模試で20番くらいまでアップして、そのままずっと特設コースのクラスでしたね。数学の模試の順位は、いい時は学年5番くらいでした。全国偏差値が60前後で安定してました。
最初の内は共通テストレベルの問題になると、解説を読んでもわからないことだらけ。よく質問してました。模試の過去問を2年分しっかりやるようにしていたので、模試の点数がよかった。それなのに学校の定期テストはサッパリ点数が上がらず、数学担当の先生も首をかしげていました。難易度の高い模試の問題はできるのですが、学校の定期テストの易しい問題ができない。
テストの後で確認すると、基礎的な知識がときどきしっちゃかめっちゃかになっているんです。わけのわからないことをしてしまう。じつは小中の算数や数学の基礎部分に穴がいっぱい開いていました。以前通っていた塾の集団授業が彼女の学力レベルには難易度が高すぎて合わなかったのだろうと思います。理解できない授業を聞いていた。成績上位の生徒に合わせた授業をしてしまうと、中位の生徒には理解できない授業になります。これは学校の授業とは反対です。学校の授業は学力中位の生徒にチューニングした授業になっているので、一部の高学力の生徒はスポイルされてしまっています。自分で難易度の高い問題集を解いていた方が、時間のロスにならなくていい。
個別指導が彼女には合っていました。過去問やってわからない箇所を塾で毎回質問してました。共通テストレベルの難易度の宿題を数学担当の先生がよく出していましたが、ビデオ解説をアップしていて、先生が発行したQRコードをスマホで読み込むとそれを視聴できるのですが、その解説も途中からわからなくなり、塾へもってきて毎回質問して、納得する、そんなことを繰り返していました。個別指導なら共通テストレベルの問題の解説をしながら、小学校算数や中学校の数学で取りこぼした基礎的な知識も整理しながら教えることができます。小学校の算数からやり直す必要はないわけです。生徒の質問に答えながら、こちらから要所要所で質問を生徒に投げたら、どこに穴が開いているのかわかります。それが個別指導のキモなのです。
彼女は質問を繰り返しながら、自分に合ったやり方を見つけてよく勉強したのです。
試行錯誤しながらなんとかやってみる、そして自分に合ったやり方を見つけてしまう。そうやって生徒は成長してしまいます。
塾先生はサポートに回るだけですよ、しっかり成長する生徒自身が偉いのです。毎年こういう生徒が出現するので、塾稼業は愉しい。
にほんブログ村
#4518 中学新入生の数学:同時に二つのことを処理するのは... Mar. 29, 2021 [52. 数学]
根室の市街化地域の中学校の新入生で分数や少数の四則演算がきちんとできる生徒は半分に満たない。
成績上位10%層は別として、中学生になって塾通いを始める生徒には、
①最初の数時間は計算問題をやらせる。
少数や分数計算の仕組みが理解できているか、速度は十分か、そのあたりのチェックからしている。なんとか少数や分数の計算問題がこなせるようになったら、2番目のステップは
②「正負の数」の予習」である
成績上位10%層は別として、中学生になって塾通いを始める生徒には、
①最初の数時間は計算問題をやらせる。
少数や分数計算の仕組みが理解できているか、速度は十分か、そのあたりのチェックからしている。なんとか少数や分数の計算問題がこなせるようになったら、2番目のステップは
②「正負の数」の予習」である
マイナスの数は中1で導入される。数の概念が拡張されるのでしっかり教えておきたい。さまざまな概念の拡張が中高の数学では重要な位置を占めている。数の概念だけに限定すれば、中1で負の数、中3で無理数が導入されて、数は実数に拡張される。高2で虚数が導入され数の概念は複素数まで拡張される。複素数の世界では指数関数が三角関数で表せるという摩訶不思議なことが起きる。数の拡張の最初のステップが中1の数学なのだ。
最初は加算、次に減算とやらせてみる。
(+2)+(-1)=
(-3)+(-5)=
(-2)-(-4)=
こういう計算を100~200題やらせて慣れたかどうか判断、慣れたら、正負両方の数を使って少数や分数の混合算へと進む。
7x(-2.4)=
-2/3x(-6)=
1/4 -(-2/3)^2 ÷4=
1-2.4=
3.9x(-0.3)=
3.9÷(-0.3)=
…
計算問題としては「複合問題」になっている。正負の数の計算と少数分数の計算の2分野という意味で、複合問題なのである。
6年生の少数や分数の計算ができるようになり、正負の整数計算は符号ミスをしなくなったのに、これら両方の要素が混ざると途端に計算規則が頭の中から飛んでしまう。この段階で少数や分数の計算問題ができなくなったり、符号ミスが多発する生徒が3割くらいいるということ。二つのことをしばらくの間は同時に処理できないのである。そういう生徒たちには1000題くらいは計算問題を解かせて、慣れさせないといけないのだが、計算に不慣れな生徒のほとんどが200題くらいの計算問題をやっただけで計算トレーニングが不徹底なまま中2となり、中3になり、定員割れした根室高校へ全員が入学しているのが現実である。根室高校ではもちろんこういうレベルまでさかのぼって教えることはない。根室西高校ではそうしていたから、計算が不慣れな生徒たちには救われる道が残されていた。
こういう計算トレーニングが不足している生徒たちは、高校生になっても計算問題に頭を使わなければならないから、文章題の複雑な問題をやれるわけがない。
どういうことか具体的に説明したい。高校受験も大学受験も、大問のところに文章(解くために必要な条件)が書かれていて、問1、問2、問3と並んでいる問題形式が多いが、問1の問題を解くときに、前段で述べられている大問の条件をすっかり忘れている生徒が根室高校普通科ではおよそ半数はいる。読んだばかりの文が次の問1の文章を読んだとたんに頭から消えている。何かに集中したとたんに、その直前までの文章が頭から消えてしまう。記憶の保持の問題である。記憶を保持できる容量が小さいのだ。
成績の良い生徒は、しばらく記憶を保持できるから、大問の条件と問題1の条件を同時に頭の中に並べで考えることができる。だから速い。そして、大筋の解法の道筋をつけたら、それに従って計算を進めていく。計算段階では脳はほとんど使っていないから、問題の条件を記憶して置けるので、問題文の条件を突合しながら、計算を進めることができる。計算には脳をほとんど使わないので、道筋からそれると違和感が働く。
言いたいことは、計算に脳を使っている生徒は数学ができるはようにはならぬということ。計算は手が勝手にやればいい、そうできるように、小学校高学年と中学校での計算トレーニングの徹底がとてつもなく重要だということ。スマホのタイマー機能を使い、10分単位の計算トレーニングを繰り返して数千題やるべきだ。
団塊世代は小学校で珠算塾へ通っている生徒が、根室で1/3くらいいた。例えば、商工会議所珠算能力検定なら、3級で乗除算は少数の問題が混ざっている。乗算・除算がそれぞれ20問、10分間で計算する。見取算が10題合計50題の計算を週に6回やれば、1年間では「50題×52週×6日=15600題」にもなる。2級から暗算10問が入る。3年間トレーニングしたら50000題は計算トレーニングをこなしてしまう。このレベルになると、四則演算に頭を使わなくて済むから、複雑な文章題を解くのにとっても有利になる。計算に投入する脳のエリアを他のことのために解放できるからだ。
こんなにしなくても小学生や中学生の時に数千問題は計算トレーニングしたほうがいい。珠算の例で言えば、採点時間を除けば、1回50題で30分である。その後で、脳を使うような複雑な問題をやればいい。
ストップウォッチで時間を測ってやると、集中力が高くなる。面白いのはこうしたトレーニングを毎日続けると意識的に集中力をコントロールできるようになるのである。集中力のスィッチ回路ができてしまう。
集中力をアップするには、日本語の本を高速音読するのもいいし、英語の教科書を高速音読してもいい。10分間で十分だ。たったそれだけで、脳は覚醒するようになる。
自分の脳のスペック(仕様)は自分がデザインできるし、デザインした通りにもっていくのはそれに適したトレーニングを毎日30分間、数年間続けたらいい。どんなことでも毎日30分間3年間は修行時間が必要だ。3年分で547.5時間ということになる。ハイスペックな脳は一度できあがると、使っていれば錆びつくことがないし、少しずつ性能が上がっていく。
昨年1月から、NHKラジオ英会話を利用して、そのままタイピングして、1/4ほどをピックアップし、英作文教材としてe-mail配信して利用している。生徒がやって来て質問があると、書いてあることの3倍くらいの説明になる。すでに4800題を超えた。3年間で10000題の問題と解説をすることになる。A4判にプリントアウトしたら680頁になっている。1頁辺り900文字ほどの量だ。
英作文も単純なトレーニングを積み上げたらいいだけ。毎日10分間の音読と英作文問題トレーニングを中高で1万題こなしたら、英検準1級に合格するのはそれほど難しくない。
要するにやり方は部活と同じで、よいトレーニングメニューで中高6年間修業できたら、まったく別世界が待っている。

にほんブログ村
最初は加算、次に減算とやらせてみる。
(+2)+(-1)=
(-3)+(-5)=
(-2)-(-4)=
こういう計算を100~200題やらせて慣れたかどうか判断、慣れたら、正負両方の数を使って少数や分数の混合算へと進む。
7x(-2.4)=
-2/3x(-6)=
1/4 -(-2/3)^2 ÷4=
1-2.4=
3.9x(-0.3)=
3.9÷(-0.3)=
…
計算問題としては「複合問題」になっている。正負の数の計算と少数分数の計算の2分野という意味で、複合問題なのである。
6年生の少数や分数の計算ができるようになり、正負の整数計算は符号ミスをしなくなったのに、これら両方の要素が混ざると途端に計算規則が頭の中から飛んでしまう。この段階で少数や分数の計算問題ができなくなったり、符号ミスが多発する生徒が3割くらいいるということ。二つのことをしばらくの間は同時に処理できないのである。そういう生徒たちには1000題くらいは計算問題を解かせて、慣れさせないといけないのだが、計算に不慣れな生徒のほとんどが200題くらいの計算問題をやっただけで計算トレーニングが不徹底なまま中2となり、中3になり、定員割れした根室高校へ全員が入学しているのが現実である。根室高校ではもちろんこういうレベルまでさかのぼって教えることはない。根室西高校ではそうしていたから、計算が不慣れな生徒たちには救われる道が残されていた。
こういう計算トレーニングが不足している生徒たちは、高校生になっても計算問題に頭を使わなければならないから、文章題の複雑な問題をやれるわけがない。
どういうことか具体的に説明したい。高校受験も大学受験も、大問のところに文章(解くために必要な条件)が書かれていて、問1、問2、問3と並んでいる問題形式が多いが、問1の問題を解くときに、前段で述べられている大問の条件をすっかり忘れている生徒が根室高校普通科ではおよそ半数はいる。読んだばかりの文が次の問1の文章を読んだとたんに頭から消えている。何かに集中したとたんに、その直前までの文章が頭から消えてしまう。記憶の保持の問題である。記憶を保持できる容量が小さいのだ。
成績の良い生徒は、しばらく記憶を保持できるから、大問の条件と問題1の条件を同時に頭の中に並べで考えることができる。だから速い。そして、大筋の解法の道筋をつけたら、それに従って計算を進めていく。計算段階では脳はほとんど使っていないから、問題の条件を記憶して置けるので、問題文の条件を突合しながら、計算を進めることができる。計算には脳をほとんど使わないので、道筋からそれると違和感が働く。
言いたいことは、計算に脳を使っている生徒は数学ができるはようにはならぬということ。計算は手が勝手にやればいい、そうできるように、小学校高学年と中学校での計算トレーニングの徹底がとてつもなく重要だということ。スマホのタイマー機能を使い、10分単位の計算トレーニングを繰り返して数千題やるべきだ。
団塊世代は小学校で珠算塾へ通っている生徒が、根室で1/3くらいいた。例えば、商工会議所珠算能力検定なら、3級で乗除算は少数の問題が混ざっている。乗算・除算がそれぞれ20問、10分間で計算する。見取算が10題合計50題の計算を週に6回やれば、1年間では「50題×52週×6日=15600題」にもなる。2級から暗算10問が入る。3年間トレーニングしたら50000題は計算トレーニングをこなしてしまう。このレベルになると、四則演算に頭を使わなくて済むから、複雑な文章題を解くのにとっても有利になる。計算に投入する脳のエリアを他のことのために解放できるからだ。
こんなにしなくても小学生や中学生の時に数千問題は計算トレーニングしたほうがいい。珠算の例で言えば、採点時間を除けば、1回50題で30分である。その後で、脳を使うような複雑な問題をやればいい。
ストップウォッチで時間を測ってやると、集中力が高くなる。面白いのはこうしたトレーニングを毎日続けると意識的に集中力をコントロールできるようになるのである。集中力のスィッチ回路ができてしまう。
集中力をアップするには、日本語の本を高速音読するのもいいし、英語の教科書を高速音読してもいい。10分間で十分だ。たったそれだけで、脳は覚醒するようになる。
自分の脳のスペック(仕様)は自分がデザインできるし、デザインした通りにもっていくのはそれに適したトレーニングを毎日30分間、数年間続けたらいい。どんなことでも毎日30分間3年間は修行時間が必要だ。3年分で547.5時間ということになる。ハイスペックな脳は一度できあがると、使っていれば錆びつくことがないし、少しずつ性能が上がっていく。
昨年1月から、NHKラジオ英会話を利用して、そのままタイピングして、1/4ほどをピックアップし、英作文教材としてe-mail配信して利用している。生徒がやって来て質問があると、書いてあることの3倍くらいの説明になる。すでに4800題を超えた。3年間で10000題の問題と解説をすることになる。A4判にプリントアウトしたら680頁になっている。1頁辺り900文字ほどの量だ。
英作文も単純なトレーニングを積み上げたらいいだけ。毎日10分間の音読と英作文問題トレーニングを中高で1万題こなしたら、英検準1級に合格するのはそれほど難しくない。
要するにやり方は部活と同じで、よいトレーニングメニューで中高6年間修業できたら、まったく別世界が待っている。
にほんブログ村
#4364 定期テストの点が取れない:C Sep. 9, 2020 [52. 数学]
#4359で紹介した生徒が定期テストをもってきた。その得点は平均点に達しなかった。なぜ?
原因を突き止めたくて間違えた個所をチェックしてたら、この2週間ほど徹底的に穴潰ししたはずのところが元に戻ってしまっていた。30点ほどそれで失っていた。ひとつづつ「これはこの前こう解説したあの事例...」、いくつかピックアップしたら様子がヘン。悔しくて、不甲斐なくて、嗚咽している。「くやしぃぃぃ!」なんて一言もいわないが、心の声が聞こえてきた。
たとえば、三角関数をtの式に置き換えて処理した問題があった。実際の式は少し違うが以下のようなもの。
y=-t^2+2t-2
たとえば、三角関数をtの式に置き換えて処理した問題があった。実際の式は少し違うが以下のようなもの。
y=-t^2+2t-2
平方完成する前にマイナスをかけてしまった。t^2-2t+2としたのである。単なる式の展開と方程式は区別しろと、xを使った2次式で、数日前に具体例で方程式の場合と式の展開の場合を説明してあった。2次の項の係数が2/3のようなとき、式の展開なのに3倍して分母を払ってしまっていた。そこは理解したのだろう。ところが、三角関数の2次関数でしかもxではなくてtの式へと文字が違うだけでそして2/3ではなくて―t^2と係数がマイナス1になっただけなのだが、試験中のストレスで違ったものに見えてしまったようだ。
そういう「隙間」に陥ったときに長年習慣になっている式の展開と方程式の解き方の混同が顔を出してしまう。中学生の時から4年間かけて習慣化して身についてしまった癖は数年かけなければとれない場合がある、性格を直すようなものだから。でも、時間をかけて治せる。この手の問題を繰り返し解いて、癖を消してしまう。相当量の問題をこなす必要がある。大丈夫だ、そのための個別指導である。かならず、数学の得点は高い所で安定する。
全国模試では英語の偏差値が一番低かった。発音はとってもいい、しかし文字の書き方に独特の癖がついてしまっている。nとtがそれぞれhとℓに見える。学校の先生も塾の先生も、どうして注意しなかったのだろう。わたしは珠算を習っただけでなく高校生の時に高橋珠算塾の高橋尚美先生に頼まれて汐見町の分塾で生徒50名ほどを教えていた経験があるから、誤読の生じるような数字の書き方はとっても気になる。また仕事でシステム開発をしていたので、プログラム仕様書を書くのに数字や英文字で誤読の生じるような書き方はしない。生徒にも誤解の生じない字体で文字を書くように指導している。いったんついてしまった癖をとるのは本人が意識して正しい文字を繰り返し書いて、身体に染み込ませるしかない。このままでは入試のときにペケにされても仕方がない。
2月から、ライン配信で改訂版の「英作文千本ノック」をやることになる。さて、どこまで化けてくれるか楽しみだ。いや、本人にやるつもりがあるのだから、こちらの指導の仕方が問われる。
いくつになっても、教えるって言うのはチャレンジだ、だから楽しい。
そういう「隙間」に陥ったときに長年習慣になっている式の展開と方程式の解き方の混同が顔を出してしまう。中学生の時から4年間かけて習慣化して身についてしまった癖は数年かけなければとれない場合がある、性格を直すようなものだから。でも、時間をかけて治せる。この手の問題を繰り返し解いて、癖を消してしまう。相当量の問題をこなす必要がある。大丈夫だ、そのための個別指導である。かならず、数学の得点は高い所で安定する。
全国模試では英語の偏差値が一番低かった。発音はとってもいい、しかし文字の書き方に独特の癖がついてしまっている。nとtがそれぞれhとℓに見える。学校の先生も塾の先生も、どうして注意しなかったのだろう。わたしは珠算を習っただけでなく高校生の時に高橋珠算塾の高橋尚美先生に頼まれて汐見町の分塾で生徒50名ほどを教えていた経験があるから、誤読の生じるような数字の書き方はとっても気になる。また仕事でシステム開発をしていたので、プログラム仕様書を書くのに数字や英文字で誤読の生じるような書き方はしない。生徒にも誤解の生じない字体で文字を書くように指導している。いったんついてしまった癖をとるのは本人が意識して正しい文字を繰り返し書いて、身体に染み込ませるしかない。このままでは入試のときにペケにされても仕方がない。
2月から、ライン配信で改訂版の「英作文千本ノック」をやることになる。さて、どこまで化けてくれるか楽しみだ。いや、本人にやるつもりがあるのだから、こちらの指導の仕方が問われる。
いくつになっても、教えるって言うのはチャレンジだ、だから楽しい。
おまけ:投稿欄でのやり取りが楽しかった記事です、話題の中心は数学。タイトルはここで採り上げた生徒の発言です。
<クリックすると検索用ページへ飛んでいきます>
⇒ 記事番号管理表
#4072 「先生、土日やってないんですか?」 Aug. 31, 2019
<クリックすると検索用ページへ飛んでいきます>
⇒ 記事番号管理表
#4359 どういうわけか成績が学年4位に急伸した女生徒 Sep. 5, 2020 [52. 数学]
あたりまえのことだが、いい大学へ進学したくて小学5年生から熟へ来る生徒もいれば、成績が振るわなくて塾へあわてて来る生徒もいる。事情は人それぞれ違っているが、いくつかの類型パターンには分けられる。
大学を目指して小学校から来る者、成績不振なので心配している親に言われて中高生になってからしかたなく塾へ来る者。看護学校へ進学を予定しているが、学力に不安があるので慌てて高校3年生になってから来る者、同級生が通塾しているので、同じ塾へ行ってみようかと思う者。通塾の動機はさまざまだが、こうした類型パターンに分けることのできる生徒は多い。
昨年8月下旬から来ている高校生がいる。通塾の動機は数学の成績が下がり始めたからだ。独力ではもうやれない、助けが必要と判断したようだ。高校生になった子どもの勉強の世話を焼ける親は稀だ、それで塾を探す。
(高校生対象の塾はたった二つだけ。数英両科目を教えている塾はニムオロ塾しかなくなった。最盛期の昭和43年ころは人口が4.9万人、いまは2.5万人に激減、高校は一つになり、実質的に高校入試が消滅したようなもの。中学生の勉強の動機、「根室高校に進学したい」は消滅した。全員が根室高校進学を保障されている。中学生の通塾はいまでは珍しい。)
来てからしばらくは全国模試の数学が50番目くらいだった。このままでは「特設コース」のAクラスから外れてしまうと生徒自身が焦っていた。気持ちはわかるよ。しばらくして数学だけは20番以内へ。そして10番台前半へと全国模試の成績アップは順調に見えた。だが、定期テストでは全国模試の結果に見合わぬ点数をとることがある。成績が安定しないのはどこかに陥穽(あな)があって、そこでつまづくからだ。だから、どこに穴があるのか見つけなければならない。
ちょうど1年たち、この前受験した模試で学年4番になったと喜んでいた。苦手の筈の国語も得点がよかったので、国数英の三科目でも学年4位だ。まわりはだれもそんなにアップしたことを知らない。ネットでパスワードを入れて自分の成績が確認できただけで、個人成績表はまだ届いていない。わたしも彼女のスマホで全国模試の結果を確認しただけ。
前々回も数学は偏差値が60に近かったので期待はしていたが、「よすぎ」、「できすぎ」と笑った。
たしかにまぐれだろう。だが、前々回偏差値が60に近く、今度は63.8だから、あながちまぐれとも言えないのである。2度も続けて偏差値が高いのは、ある程度力のついてきた証左である。定期テストよりも全国模試のほうが問題の難易度は格段に高いから、「定期テストー20」くらいが全国模試の点数となる。英語は全国平均点に2点足りないから偏差値50にちょっとだけ足りぬ。まだしばらくダメだろう。英語にまとまめて投入する時間が確保できない。この生徒はいろいろやっていていまとっても忙しいのだ。年を越したらLine配信の「英作文千本ノック」に参加できるかな?いまのところ文型でタイプ分けした基礎英作文も一度もやってきたことがない。(笑)
今週根室高校は前期期末テストを実施したが、この生徒は数Bの数列の漸化式のところの式の整理が苦手なので、説明してほしいと要求があった。解答を見てもどのような処理をしてこうなるのかわからないと本人が言うので解答集の当該箇所をみた。因数分解と分数が混じっており、ちょっと複雑な処理をしなければいけない、ここだったのか、分数計算が関連するところで混乱することが分かった。式の展開をしている途中で、分母と同じ数をかけて整数の式にしてしまう。式の展開と等式の違いがわかっていなかった。つまり等式の概念が理解できていなかった。これも今回しっかり解説した。数字の分数計算ならやれても、文字式になったとたんに違うものに見えてしまう生徒は多い。数字の式のときと同じ計算規則でやればいいのだが、なぜか混乱して自分独自の計算ルールを編み出して適用してしまう。こういう生徒は個別に診て今まで積み上げた知識を整理してやらないといつまでも混乱から抜け出せない。集団指導では救えないタイプである。
数Ⅱの軌跡のところも、平方完成するときに、カッコの中が分数になると途端にヘンな計算をしだす。計算が分数交じりで複雑になると途端にエイヤと計算規則を超越してしまう。複雑な計算のストレスに弱い、やはり分数計算に問題があった。高校生だから、ちゃんと説明すれば理解できるが、手間がずいぶんかかった。曖昧になっている計算規則は頭の中で、複雑な計算になった途端に独自の計算規則へ突然飛んでしまうように習慣になっているから、それを外さなくてはいけない。間違えた個所を使って、繰り返し正しい計算の規則を説明し、その習慣化されてしまっている”ワープ”を消すのが大変なのだ。好い点数が獲りたくてすなおによく聞くからめんこい。(笑)
三角関数も範囲だったが、n・sineΘ/3やΘのところが(Θ+π/2)という類のグラフがかけないというので、これも丁寧に解説し、何度も描いてもらった。y軸が0や±1の箇所はΘの値を記入しないといけないが、これも分数計算を伴なう。
厄介だったのはtanΘのグラフである。これもΘのところが分数だったり、(Θ-π/3)だったりするとどうやってよいのかわからなくなっていた。計算を繰り返して、何度も描いてみたら、なんとかやれるようになった。試験本番で完璧にやれるようになるのは、理解しただけではダメで、怪しいところは何度も繰り返しやってみて、手に覚えこませなければならない。家でもやっていれば成果を期待してよさそうだ、ぎりぎりだったから家でなんども練習する時間がとれただろうか?80点獲れたら素晴らしいと思う、80点をクリアできれば、自信がついてじきに90点獲れるようになる。
塾用問題集シリウスのコンパクトな解説を見ただけですっとできる生徒もいる。手間のかからない生徒である。ときどき質問が出るからそれに応えるだけで十分。その生徒は数Ⅲ青チャートを5か月でやり終えたが、質問は10個もあっただろうか?問題集の例題を見ただけですぐに演習問題が解けてしまう。だから、余計な説明はしないほうがいい。
偏差値70を超えている生徒でも学力や理解力は勉強のさせ方で3年5年とたつうちにまるで違ってくる。塾への依存心を植え付けてはいけない。予習方式で小5の1月からやってきてから、高校生になったらシリウスのコンパクトな解説を独力で読むだけで理解は十分で、あとは自力で問題演習に取り組んでいる。だから、難易度の高い問題でわけがわからなくなったときだけ、生徒の質問に丁寧に応じてやるだけでいい。手とり足取り教えたら、教えてもらわないと理解できないタイプに育つ。
依存心が強い生徒は質問があっても、どこがわからないのか確認しただけで「あと5分だけ考えてみろ」ということがある。複雑そうなので面倒くさくて思考停止し質問する生徒もいるからだ。もうすこし「わからない」という状態を我慢出来たら、案外、正解に到達できる。そのあたりの見極めが個別指導の楽しいところ。子どもたちの理解力は千差万別だから、学力や理解力にあった教え方を工夫すればいいだけ。
教えてその時は理解できても、家で学習しない生徒はお手上げである。翌週、また似たようなことを教えることになる。スマホの虜になってしまった生徒たちから、帰宅してから10時までは取り上げてもらうように話し合っても数日で、たいがい破綻する。自覚を俟つしかないこともある。休みが多くて休塾を勧告して、実際に1年間休塾扱いした生徒もいる。
成績が急伸したこの生徒は全国模試の数学の点数はいいのだが、定期テストが模試の点数くらいしか獲れない、めずらしいタイプ。普通は全国模試が60点を超えたら、定期テストは90点越せるのがあたりまえである。まだそこは無理だろう、ワンステップ必要だ。そんなに簡単にいままでの習慣を消すことはできない。何年もかかって身についてしまった習慣を消し去るのはそれほど困難なのである。でも、もう克服すべき課題ははっきり見えているから、今回の定期テストは80点越えを期待している。
小学校で分数計算を学びそこなうと、高校生になってまぐれにせよ女子の中では全国模試の数学が学年トップでも、アキレス腱を抱えている生徒がいるのは事実である。どれくらいいるのだろう?高校では分数計算を教えないので、こういう生徒たちは放置されている。それでも模試でときどきいい点が取れるのだから不思議だ。
大学を目指して小学校から来る者、成績不振なので心配している親に言われて中高生になってからしかたなく塾へ来る者。看護学校へ進学を予定しているが、学力に不安があるので慌てて高校3年生になってから来る者、同級生が通塾しているので、同じ塾へ行ってみようかと思う者。通塾の動機はさまざまだが、こうした類型パターンに分けることのできる生徒は多い。
昨年8月下旬から来ている高校生がいる。通塾の動機は数学の成績が下がり始めたからだ。独力ではもうやれない、助けが必要と判断したようだ。高校生になった子どもの勉強の世話を焼ける親は稀だ、それで塾を探す。
(高校生対象の塾はたった二つだけ。数英両科目を教えている塾はニムオロ塾しかなくなった。最盛期の昭和43年ころは人口が4.9万人、いまは2.5万人に激減、高校は一つになり、実質的に高校入試が消滅したようなもの。中学生の勉強の動機、「根室高校に進学したい」は消滅した。全員が根室高校進学を保障されている。中学生の通塾はいまでは珍しい。)
来てからしばらくは全国模試の数学が50番目くらいだった。このままでは「特設コース」のAクラスから外れてしまうと生徒自身が焦っていた。気持ちはわかるよ。しばらくして数学だけは20番以内へ。そして10番台前半へと全国模試の成績アップは順調に見えた。だが、定期テストでは全国模試の結果に見合わぬ点数をとることがある。成績が安定しないのはどこかに陥穽(あな)があって、そこでつまづくからだ。だから、どこに穴があるのか見つけなければならない。
ちょうど1年たち、この前受験した模試で学年4番になったと喜んでいた。苦手の筈の国語も得点がよかったので、国数英の三科目でも学年4位だ。まわりはだれもそんなにアップしたことを知らない。ネットでパスワードを入れて自分の成績が確認できただけで、個人成績表はまだ届いていない。わたしも彼女のスマホで全国模試の結果を確認しただけ。
前々回も数学は偏差値が60に近かったので期待はしていたが、「よすぎ」、「できすぎ」と笑った。
たしかにまぐれだろう。だが、前々回偏差値が60に近く、今度は63.8だから、あながちまぐれとも言えないのである。2度も続けて偏差値が高いのは、ある程度力のついてきた証左である。定期テストよりも全国模試のほうが問題の難易度は格段に高いから、「定期テストー20」くらいが全国模試の点数となる。英語は全国平均点に2点足りないから偏差値50にちょっとだけ足りぬ。まだしばらくダメだろう。英語にまとまめて投入する時間が確保できない。この生徒はいろいろやっていていまとっても忙しいのだ。年を越したらLine配信の「英作文千本ノック」に参加できるかな?いまのところ文型でタイプ分けした基礎英作文も一度もやってきたことがない。(笑)
今週根室高校は前期期末テストを実施したが、この生徒は数Bの数列の漸化式のところの式の整理が苦手なので、説明してほしいと要求があった。解答を見てもどのような処理をしてこうなるのかわからないと本人が言うので解答集の当該箇所をみた。因数分解と分数が混じっており、ちょっと複雑な処理をしなければいけない、ここだったのか、分数計算が関連するところで混乱することが分かった。式の展開をしている途中で、分母と同じ数をかけて整数の式にしてしまう。式の展開と等式の違いがわかっていなかった。つまり等式の概念が理解できていなかった。これも今回しっかり解説した。数字の分数計算ならやれても、文字式になったとたんに違うものに見えてしまう生徒は多い。数字の式のときと同じ計算規則でやればいいのだが、なぜか混乱して自分独自の計算ルールを編み出して適用してしまう。こういう生徒は個別に診て今まで積み上げた知識を整理してやらないといつまでも混乱から抜け出せない。集団指導では救えないタイプである。
数Ⅱの軌跡のところも、平方完成するときに、カッコの中が分数になると途端にヘンな計算をしだす。計算が分数交じりで複雑になると途端にエイヤと計算規則を超越してしまう。複雑な計算のストレスに弱い、やはり分数計算に問題があった。高校生だから、ちゃんと説明すれば理解できるが、手間がずいぶんかかった。曖昧になっている計算規則は頭の中で、複雑な計算になった途端に独自の計算規則へ突然飛んでしまうように習慣になっているから、それを外さなくてはいけない。間違えた個所を使って、繰り返し正しい計算の規則を説明し、その習慣化されてしまっている”ワープ”を消すのが大変なのだ。好い点数が獲りたくてすなおによく聞くからめんこい。(笑)
三角関数も範囲だったが、n・sineΘ/3やΘのところが(Θ+π/2)という類のグラフがかけないというので、これも丁寧に解説し、何度も描いてもらった。y軸が0や±1の箇所はΘの値を記入しないといけないが、これも分数計算を伴なう。
厄介だったのはtanΘのグラフである。これもΘのところが分数だったり、(Θ-π/3)だったりするとどうやってよいのかわからなくなっていた。計算を繰り返して、何度も描いてみたら、なんとかやれるようになった。試験本番で完璧にやれるようになるのは、理解しただけではダメで、怪しいところは何度も繰り返しやってみて、手に覚えこませなければならない。家でもやっていれば成果を期待してよさそうだ、ぎりぎりだったから家でなんども練習する時間がとれただろうか?80点獲れたら素晴らしいと思う、80点をクリアできれば、自信がついてじきに90点獲れるようになる。
塾用問題集シリウスのコンパクトな解説を見ただけですっとできる生徒もいる。手間のかからない生徒である。ときどき質問が出るからそれに応えるだけで十分。その生徒は数Ⅲ青チャートを5か月でやり終えたが、質問は10個もあっただろうか?問題集の例題を見ただけですぐに演習問題が解けてしまう。だから、余計な説明はしないほうがいい。
偏差値70を超えている生徒でも学力や理解力は勉強のさせ方で3年5年とたつうちにまるで違ってくる。塾への依存心を植え付けてはいけない。予習方式で小5の1月からやってきてから、高校生になったらシリウスのコンパクトな解説を独力で読むだけで理解は十分で、あとは自力で問題演習に取り組んでいる。だから、難易度の高い問題でわけがわからなくなったときだけ、生徒の質問に丁寧に応じてやるだけでいい。手とり足取り教えたら、教えてもらわないと理解できないタイプに育つ。
依存心が強い生徒は質問があっても、どこがわからないのか確認しただけで「あと5分だけ考えてみろ」ということがある。複雑そうなので面倒くさくて思考停止し質問する生徒もいるからだ。もうすこし「わからない」という状態を我慢出来たら、案外、正解に到達できる。そのあたりの見極めが個別指導の楽しいところ。子どもたちの理解力は千差万別だから、学力や理解力にあった教え方を工夫すればいいだけ。
教えてその時は理解できても、家で学習しない生徒はお手上げである。翌週、また似たようなことを教えることになる。スマホの虜になってしまった生徒たちから、帰宅してから10時までは取り上げてもらうように話し合っても数日で、たいがい破綻する。自覚を俟つしかないこともある。休みが多くて休塾を勧告して、実際に1年間休塾扱いした生徒もいる。
成績が急伸したこの生徒は全国模試の数学の点数はいいのだが、定期テストが模試の点数くらいしか獲れない、めずらしいタイプ。普通は全国模試が60点を超えたら、定期テストは90点越せるのがあたりまえである。まだそこは無理だろう、ワンステップ必要だ。そんなに簡単にいままでの習慣を消すことはできない。何年もかかって身についてしまった習慣を消し去るのはそれほど困難なのである。でも、もう克服すべき課題ははっきり見えているから、今回の定期テストは80点越えを期待している。
小学校で分数計算を学びそこなうと、高校生になってまぐれにせよ女子の中では全国模試の数学が学年トップでも、アキレス腱を抱えている生徒がいるのは事実である。どれくらいいるのだろう?高校では分数計算を教えないので、こういう生徒たちは放置されている。それでも模試でときどきいい点が取れるのだから不思議だ。
根室の中学校で分数計算が苦手な生徒は半数はいそうだ。中学校の段階で、分数の苦手な生徒を補習で救ってあげられたら、生徒たちの数学の学力はずいぶんアップするだろう。根室市内の市街化地域の3中学校の昨年の学力テストの数学の平均点は15-16点(60点満点)である。釧路根室管内の18中学校の学力テストデータでは両管内で最低レベルにある。平均点以下の生徒たちに、標準的な難易度の普通科の数学を理解するのは無理がある。中学校の学力テストで40-50点は採れるようにしておきたい。数ⅡBはそれくらいでないと、独力で理解できない。そうした生徒はいまでは1割もいない。釧路根室管内で最低レベル、この現状をしっかり見つめたい。
青字の部分をクリックすれば、釧路根室管内の18校の昨年「9月の学力テスト総合Aの学校別・科目別平均点データが確認できる。
*
⇒ 記事番号管理表

にほんブログ村
青字の部分をクリックすれば、釧路根室管内の18校の昨年「9月の学力テスト総合Aの学校別・科目別平均点データが確認できる。
*
#4099 学力テスト総合A18校科目別データ
<クリックすると検索用ページへ飛んでいきます>⇒ 記事番号管理表
にほんブログ村
#4353 数学嫌いの生徒の「数学って役にたつの?」という問いをめぐって Aug. 30, 2020 [52. 数学]
数学が嫌いで「何に役にたつのか?」という生徒はいるけど、社会や理科に対して同じことを言う生徒がいないという高校の数学の先生の意見に対して、社会は暗記科目でつまらないという理系の大人の意見あり。また、音楽・図工・体育に関しては生きてくのに必要ないから、「これって役にたつの?」なんてことすら聞かないというのは別の理系の人のご意見。必要なのは国算社理英の五科目のみ、芸体三科目は役に立たぬということか。
FB上で今日なされた議論です。あなたの意見はどうですか?
FB上で今日なされた議論です。あなたの意見はどうですか?
意見は十人十色。
だから、意見の異なる人との対話は楽しい。
リアルタイムで空間の制限を超えて分野の異なる人たちと議論ができるのはとっても便利。
SNSは使いようで役に立つ。(笑)
以下は網掛け部分はFBに書き込んだわたしの意見です。
もちろん、数学だって、音楽だって、図工だって、体育だって役に立ちます。文系科目(たとえば、原価計算論)にだって微分方程式が出てくるし、大学教養科目にある統計学は数学が理解できなければ無理。Σ記号を使った式がふんだんに出てきます。確率分布や推測統計は数Bの範囲ですが、高校の授業ではやっていません。統計学には数Ⅱと数Bの知識が必要です。統計データは分野を問わず様々な専門書にでてきます。できれば選択科目になっている数Ⅲまでしっかりやっておいた方がいい。欲を言えば線形代数への橋渡しに行列式もやっておいた方がいいのです。いまでは高校数学からなくなってしまいました。社会人になって仕事をし始めると高校数学の範囲では足りませんから、あとは独学でやることになります。数学の概念と世界が広がるので、複素関数の初歩ぐらいは高校と大学を通じて趣味の範囲でもやっておくべきですね。文系の学生でそこまで好奇心を広げられる生徒は千人に一人ぐらいの割合でしか出現しないでしょう。きりがないのです。
悲しい時は、悲しい音楽を聴いて涙を流したらいいし、楽しい時は楽しい音楽を聴けばいい。音楽は短歌や俳句や詩の中にも流れています。情緒に関する部分はこころの核心部分ですから、知的活動を左右する部分です。音楽や図工はとっても大事です。国算社理英よりも重要性が低いなんてことはありません。
身体が柔軟でなければケガが多くなるし、年老いてから故障が多くなります。体育だってやりようで役に立つのです。
マウンテンバイクでT字路を左折するときに右折車が斜めに曲がって来て進路をふさがれました。とっさに急ブレーキ、前輪がロックして見事に一回転してアスファルトへ。とっさに頭を引っ込めて受け身してました。身体ってしっかり記憶していて、何十年たってもとっさに反応してくれます。運悪く着地したところに25㎝の高さの縁石があり左腿をしたたかに打ち、見る間に腫れましたが、骨折はしてませんでした。受け身ができなければ、かなりのケガでしたよ。わたしの場合は体育は役に立ってます。昨年は逆上がりができないという幼稚園の孫に実演して見せましたから。たのしかった。「ジジできるんだ」って大はしゃぎでした。(笑) 体操教室に通っていましたが、孫のやるストレッチを真似してやって見せたら、目をまん丸くして、「ジジ、どうしてできるの?」って一緒に遊んでくれました。孫よりやわらかいのです。ストレッチをするときの呼吸の仕方を教えてあげました。
学びは授業だけではありません。生徒会会計をやったことがその後の人生の武器になりました。各部の部長と副部長を生徒会室に呼び、予算折衝をしてましたから、会社勤めをして中途採用でいきなり予算編成を任されてもOKでした。公平にやる、急所は生徒会会計の仕事と同じなのです。従業員が200人でも、3000人でも一緒です。予算編成と予算管理の本質は従業員1万人の企業でも同じ。それを支えるシステムに違いがあるだけです。企業規模に合わせたシステムが創れる専門知識と経験があればいい。そういう場ではより高度な学力と経験が必要になります。経営改革を目的とした経営管理や経営企画ということになるともう少し専門知識の範囲と経験のレベルが上がります。
根室高校の校則改正(丸刈り坊主頭を廃止)の経験も役に立ちました。理不尽な旧弊はドンドン変えたらいい。経営改革とはそう言うことです。高校の校則改正も企業の経営改革も本質は一緒です。質の良い経験を積んでいれば、赤字の会社も黒字にできます、実際にいくつもやってきました。
質の良い経験を中学・高校時代にしっかり積んでください。部活も生徒会活動も大事です、社会人になってからそういう経験智がモノを言います。
ところで、わたしも数学を教えていますが、「数学する」って楽しいから教えています。出力(授業で教えていること)以上に入力(学び)しています。英語もそうです。ハラリのSapiensの原書講読が左サイドバーのカテゴリー欄にあるので、そこ「44-3. 原書講読講座 Sapiens(41)」をクリックして読んでいただければ、生徒の疑問に答えながら原書を読む愉しさがきっとお分かりいただけます。
どんな科目も将来の仕事にしっかり役にたちますから、深く学んで楽しんでください。
(ここまで、この文書作成におおよそ30分かかりました)
----------------------------------------------------------
9/29追記:新型コロナ(COVID-19)の真陽性や擬陽性を理解するには高校数学「数A」の条件付き確率が理解できないと、話が呑み込めません。数学はとっても役に立つのです。
<クリックすると検索用ページへ飛んでいきます>
⇒ 記事番号管理表

にほんブログ村
だから、意見の異なる人との対話は楽しい。
リアルタイムで空間の制限を超えて分野の異なる人たちと議論ができるのはとっても便利。
SNSは使いようで役に立つ。(笑)
以下は網掛け部分はFBに書き込んだわたしの意見です。
歴史はとっても面白い。よく眺めてみると、おおよそ400年ごとに日本は大きな歴史的転換点を迎えてきたことに気が付く。いまそういう転換点の時代を迎えている。パラダイムシフトが起きている中で生きているんだ。
学校の試験なんかを基準に考えていると、どの科目だってつまらない。授業で教えてもらったことを超えて、好奇心に任せて何を学び取るかが勝負だろう。
古典文学だって、詩歌だって、経済学だって、統計学だって、コンピュータシステムだって、好奇心があれば愉しいものに変わる。
つまらない教科と感じたら、それはつまらない勉強の仕方をしているからだろう。
数学にも文学にも社会科にも理科にも面白さの差は感じません。
役に立つ勉強の仕方をすればどの教科も役に立つし、底の浅いいい加減な勉強の仕方に終始すればまったく役には立たないとわたしは思ってます。
そして学びの半分くらいは経験からかな。学校の授業で教えてもらえることはほんのわずかです。
もちろん、数学だって、音楽だって、図工だって、体育だって役に立ちます。文系科目(たとえば、原価計算論)にだって微分方程式が出てくるし、大学教養科目にある統計学は数学が理解できなければ無理。Σ記号を使った式がふんだんに出てきます。確率分布や推測統計は数Bの範囲ですが、高校の授業ではやっていません。統計学には数Ⅱと数Bの知識が必要です。統計データは分野を問わず様々な専門書にでてきます。できれば選択科目になっている数Ⅲまでしっかりやっておいた方がいい。欲を言えば線形代数への橋渡しに行列式もやっておいた方がいいのです。いまでは高校数学からなくなってしまいました。社会人になって仕事をし始めると高校数学の範囲では足りませんから、あとは独学でやることになります。数学の概念と世界が広がるので、複素関数の初歩ぐらいは高校と大学を通じて趣味の範囲でもやっておくべきですね。文系の学生でそこまで好奇心を広げられる生徒は千人に一人ぐらいの割合でしか出現しないでしょう。きりがないのです。
悲しい時は、悲しい音楽を聴いて涙を流したらいいし、楽しい時は楽しい音楽を聴けばいい。音楽は短歌や俳句や詩の中にも流れています。情緒に関する部分はこころの核心部分ですから、知的活動を左右する部分です。音楽や図工はとっても大事です。国算社理英よりも重要性が低いなんてことはありません。
身体が柔軟でなければケガが多くなるし、年老いてから故障が多くなります。体育だってやりようで役に立つのです。
マウンテンバイクでT字路を左折するときに右折車が斜めに曲がって来て進路をふさがれました。とっさに急ブレーキ、前輪がロックして見事に一回転してアスファルトへ。とっさに頭を引っ込めて受け身してました。身体ってしっかり記憶していて、何十年たってもとっさに反応してくれます。運悪く着地したところに25㎝の高さの縁石があり左腿をしたたかに打ち、見る間に腫れましたが、骨折はしてませんでした。受け身ができなければ、かなりのケガでしたよ。わたしの場合は体育は役に立ってます。昨年は逆上がりができないという幼稚園の孫に実演して見せましたから。たのしかった。「ジジできるんだ」って大はしゃぎでした。(笑) 体操教室に通っていましたが、孫のやるストレッチを真似してやって見せたら、目をまん丸くして、「ジジ、どうしてできるの?」って一緒に遊んでくれました。孫よりやわらかいのです。ストレッチをするときの呼吸の仕方を教えてあげました。
学びは授業だけではありません。生徒会会計をやったことがその後の人生の武器になりました。各部の部長と副部長を生徒会室に呼び、予算折衝をしてましたから、会社勤めをして中途採用でいきなり予算編成を任されてもOKでした。公平にやる、急所は生徒会会計の仕事と同じなのです。従業員が200人でも、3000人でも一緒です。予算編成と予算管理の本質は従業員1万人の企業でも同じ。それを支えるシステムに違いがあるだけです。企業規模に合わせたシステムが創れる専門知識と経験があればいい。そういう場ではより高度な学力と経験が必要になります。経営改革を目的とした経営管理や経営企画ということになるともう少し専門知識の範囲と経験のレベルが上がります。
根室高校の校則改正(丸刈り坊主頭を廃止)の経験も役に立ちました。理不尽な旧弊はドンドン変えたらいい。経営改革とはそう言うことです。高校の校則改正も企業の経営改革も本質は一緒です。質の良い経験を積んでいれば、赤字の会社も黒字にできます、実際にいくつもやってきました。
質の良い経験を中学・高校時代にしっかり積んでください。部活も生徒会活動も大事です、社会人になってからそういう経験智がモノを言います。
ところで、わたしも数学を教えていますが、「数学する」って楽しいから教えています。出力(授業で教えていること)以上に入力(学び)しています。英語もそうです。ハラリのSapiensの原書講読が左サイドバーのカテゴリー欄にあるので、そこ「44-3. 原書講読講座 Sapiens(41)」をクリックして読んでいただければ、生徒の疑問に答えながら原書を読む愉しさがきっとお分かりいただけます。
どんな科目も将来の仕事にしっかり役にたちますから、深く学んで楽しんでください。
(ここまで、この文書作成におおよそ30分かかりました)
----------------------------------------------------------
9/29追記:新型コロナ(COVID-19)の真陽性や擬陽性を理解するには高校数学「数A」の条件付き確率が理解できないと、話が呑み込めません。数学はとっても役に立つのです。
#4375 新型コロナPCR検査陽性者のなかで真の感染者の割合はどれだけか?
<クリックすると検索用ページへ飛んでいきます>
⇒ 記事番号管理表
にほんブログ村
#4268 面白い循環小数問題&記数法問題 June 12, 2020 [52. 数学]
3年生の生徒が進学講習のプリントをもってきた。その中に面白そうな問題があった。
問:ある整数の逆数をとったら、0.abcabcabc...と3桁の循環小数となった。その整数の最小値と2番目に小さい値を求めよ。
改題して「そのときのabcの値を求めよ」と付け加えたらもっと面白くなる。
答えは、27と37である。(a,b,c)=(0,3,7) , (0,2,7)
この生徒、循環小数は習っていないと主張していたが、数1の教科書にあるから、やっている。見せたら「あ、ある、ほんとうだ」、忘れていただけ。ちょっとやっただけだから2年たつと普通は忘れてしまっている。そしてこういう難易度の高い問題は根室高校1年生の授業ではやっていません。忘れてたのもあるけどやっていないといった方が正鵠を射ているのでしょう。かつてやったことを思い出し、複合問題にチャレンジするには好いプリントです。
(数Ⅲをやっている生徒からは、逆関数の積分の問題の質問が出ました。このところやっている問題は特殊な問題が多いから、基本を忘れてただけ。30秒の解説で理解してました。1/14から『青チャート数Ⅲ』全問制覇をし始めて、6月末までに終了が当初スケジュールですが、1週間余して終われそうです。この生徒は意志の強さをほめたい。)
プリントには2進数の除算問題も載ってました、どうやったらいいのか鳩が豆鉄砲を食らったような顔で質問していましたが、十進数と同じように割り算したらいいだけ。やって見せたら余りがゼロになったところでピンポーン!黒板見ないで自分でやってみて「できました!」。8進数の加算や減算問題は、繰り上がりや繰り下がりを8でやるだけ、縦に並べて計算すればすぐにできる。横計算でやると難問になる。筆算は小学校でも縦でやったでしょ。こちらも慣れておかないと、大学受験本番で出題されたら、時間を食ってしまい痛い目に合う。今年の夏休みは2週間ほどしかなく短いが毎日12時間勉強して、忘れていたものを思い出したらいい。
20代後半(1978年)に、好奇心からマイコンの本を読み漁って、2進数、8進数、16進数の計算をしたのが懐かしい。当時はパソコンはおもちゃ同然。社内にあったコモドール製パソコンは、押しても戻ってこないキーがあったほど粗雑な造りでした。HP社のマイクロ波計測器の制御とデータ処理部に使われていたパソコンは当時200万円くらいしました。これは優れものですが、個人ユースでは買ってもらえません。(笑)
オフコンとワープロが仕事で使われ始めてました。1979年に三菱電機製のA4縦型のワープロを東京営業所で見積作成用に導入しましたが200万円しました。1982年10月にNEC9800シリーズのパソコンが売り出されたときには驚きでした。キーボードがコモドール製品とは比較にならぬほどしっかりしてました。スプリングの品質が違っていたのでしょう。
中途入社してすぐに5つのプロジェクトを任され、自社の経営分析と収益構造を変える具体案を作り実行するために、かなりの量の統計計算が必要で、数日間、朝から晩まで電卓叩いて計算してましたが、そのままでは埒が明かず、どうしようかと思っていたら、HP社のHP67とプリンタ付きのHP97を入社1か月目と2か月目に関周社長が米国出張で買ってきてくれました。朝出社すると机の上に置いてある、うれしかった。秘書に尋ねると「社長がebisuさんに使えって置いてきました」。当時11万円と22万円もした高額の科学技術用プログラマブル計算機でした。一日中計算に明け暮れていたのが、プログラムを組んでしまうとデータ入力とチェックだけでいいので30分で終わってしまったのは感激でした。時間が短縮できるので統計計算量が数倍に増えました。線形回帰分析をベースに、経営分析用の25ゲージのレーダ・チャートを開発しました。組んだプログラムはテストデータでチェック済みですから、計算の確認がいらない。プロジェクト5つ抱えていても問題がなくなりました。収益構造を変えることを目標にシステム化(為替管理、円定価表システム、納期管理システム、仕入在庫管理など)をいくつかやったので、3年後には会社の売上高経常利益率が7%ほどアップしてました。これらのシステムは円定価見積レート、仕入レート、決済レートで連動していました。仕入れと営業実務が劇的に変わりました。
400頁の英文のマニュアル2冊を1週間で読み切り統計関係の数値プログラミングをマスターし、その後2年間の間にさらに2言語プログラミング言語をマスターして仕事で使いました。3年目には会計情報統合システム分野では国内トップレベルのSEと互角に仕事してました。5年目には為替管理や簿記や原価計算、経営分析、在庫管理、初等統計学などの専門知識がある分だけこちらが有利、国内トップレベルのSEを超えましたね。その都度一緒に仕事するソフトハウス(オービック⇒日本電気情報サービス⇒NCD社)は代わりましたが、スキルが上がるとSEたちは何でも言うこと聞いてくれました。8か月で臨床検査最大手SRLの会計情報統合システムが本稼働した後、「暇だからプログラミングやろうかな」って言ったら、「内部設計やプログラミングはわたしたちがやるので、ebisuさんは実務デザインと仕様書書いてください」って。(笑)
コンピュータを扱えることはあたりまえ、それ以外の専門知識が大事。国語と数学と英語の勉強をちゃんとやっておけば、コンピュータ関係の専門書は必要な時に独力で読めるし、仕事で使えばスキルも短期間で飛躍的に伸びます。だから高校生のときには国語と数学と英語の勉強をしっかりやっておこう。大学では専門分野を極めよう。簡単なプログラミングはとっくにブラックの世界ですよ。雇用の安定しない非正規・低賃金です。ゲームソフトの世界も恐らく同じでしょうよ。どうか高校生の皆さんは高額報酬分野を目指して勉強してください。それには国語と数学と英語が大事です。情報の勉強なんか社会人になってからでも独学でやれます。仕事でつかえる環境があればスキルはぐんぐん伸びます。スキルの高いSEと仕事する機会があれば、技術は盗めます。一緒に仕事して見ただけでわかるんです。
さて、高校数学の勉強の話に戻りましょう。ふだんやっている問題集に良問には「良」のマークを付け、できなかった問題には「レ点」をつけてあれば、効率的に復習できます。マークを付けた問題でも2度目にやって十分理解したら、マークに二重線を引いておけば、3度目はパスできます。こうして問題の分量を減らしていけば数分の一の時間で復習できまります。時間は一日24時間しかないから、いかに効率的に復習するかが3年次の学習効果を決定します。ふだんの勉強方式は予習方式です。これが一番効率がいい。なぜかって?習っていないところを予習してあると、どこがわからないかがはっきりしますから、学校の授業は分からなかったところに集中して聴けばいい、つまり復習になってしまうからです。そういう勉強の仕方が学力アップの効率が高い。
<余談:転職≒天職>
1978年の大学新卒の初任給は105,500円でした。産業用エレクトロニクス輸入専門商社の関周社長が入社早々に買ってくれたHP97は22万円ですからずいぶん高い製品だったのです。
本社は日本橋人形町、大学院卒の中途入社でした、初任給は2.5倍ほどいただいたのではなかったか。仕事は期待に応えたと思います。五年後にこの会社を辞めて、職探しにリクルート社の人材斡旋で選んだうちにフェアチャイルドジャパンがありました、経理課長職で年収850万円でした。当時の大卒初任給は135,800円ですから、年収220万円程度です。外資の半導体製造企業は日本企業に勝てそうもないのでいずれ撤退になると判断。プレジデント社とスキルの高い上場準備要員を募集していた臨床最大手SRLに絞って、5年分の決算情報をみて、両方の会社を訪問しました。プレジデント社は赤坂に事務所がありました、雑誌の編集の仕事です、経営や経済記事が中心の雑誌ですから向いていたかもしれません。
上場準備中のSRLはシステム開発の高度なスキルが生かせます。担当できる社員がいなくて困ってました。SRLは西新宿の超高層ビル22階が本社、いまでこそ都庁の手前ですが、当時は都庁は丸の内で西新宿にはまだ移転してません。ビルと業績でSRLに決めました。高校卒業して根室から出て行って、都会で仕事ですから、超高層ビルで一度仕事してみたかった、それだけ。(笑)
その後、横浜の療養型病院の常務理事となり、病棟建て替えをやり終え、また転職。外食産業の別の会社で経営企画次長として銀座3丁目でも仕事することになります。
根室へ戻って来てから、東北の会社からお誘いが一度ありましたが、いくらなんでももう転職はナシです。体力がありません、そのうちにふるさとの土になります。(笑)
https://nenji-toukei.com/n/kiji/10021)

にほんブログ村
問:ある整数の逆数をとったら、0.abcabcabc...と3桁の循環小数となった。その整数の最小値と2番目に小さい値を求めよ。
改題して「そのときのabcの値を求めよ」と付け加えたらもっと面白くなる。
答えは、27と37である。(a,b,c)=(0,3,7) , (0,2,7)
この生徒、循環小数は習っていないと主張していたが、数1の教科書にあるから、やっている。見せたら「あ、ある、ほんとうだ」、忘れていただけ。ちょっとやっただけだから2年たつと普通は忘れてしまっている。そしてこういう難易度の高い問題は根室高校1年生の授業ではやっていません。忘れてたのもあるけどやっていないといった方が正鵠を射ているのでしょう。かつてやったことを思い出し、複合問題にチャレンジするには好いプリントです。
(数Ⅲをやっている生徒からは、逆関数の積分の問題の質問が出ました。このところやっている問題は特殊な問題が多いから、基本を忘れてただけ。30秒の解説で理解してました。1/14から『青チャート数Ⅲ』全問制覇をし始めて、6月末までに終了が当初スケジュールですが、1週間余して終われそうです。この生徒は意志の強さをほめたい。)
プリントには2進数の除算問題も載ってました、どうやったらいいのか鳩が豆鉄砲を食らったような顔で質問していましたが、十進数と同じように割り算したらいいだけ。やって見せたら余りがゼロになったところでピンポーン!黒板見ないで自分でやってみて「できました!」。8進数の加算や減算問題は、繰り上がりや繰り下がりを8でやるだけ、縦に並べて計算すればすぐにできる。横計算でやると難問になる。筆算は小学校でも縦でやったでしょ。こちらも慣れておかないと、大学受験本番で出題されたら、時間を食ってしまい痛い目に合う。今年の夏休みは2週間ほどしかなく短いが毎日12時間勉強して、忘れていたものを思い出したらいい。
20代後半(1978年)に、好奇心からマイコンの本を読み漁って、2進数、8進数、16進数の計算をしたのが懐かしい。当時はパソコンはおもちゃ同然。社内にあったコモドール製パソコンは、押しても戻ってこないキーがあったほど粗雑な造りでした。HP社のマイクロ波計測器の制御とデータ処理部に使われていたパソコンは当時200万円くらいしました。これは優れものですが、個人ユースでは買ってもらえません。(笑)
オフコンとワープロが仕事で使われ始めてました。1979年に三菱電機製のA4縦型のワープロを東京営業所で見積作成用に導入しましたが200万円しました。1982年10月にNEC9800シリーズのパソコンが売り出されたときには驚きでした。キーボードがコモドール製品とは比較にならぬほどしっかりしてました。スプリングの品質が違っていたのでしょう。
中途入社してすぐに5つのプロジェクトを任され、自社の経営分析と収益構造を変える具体案を作り実行するために、かなりの量の統計計算が必要で、数日間、朝から晩まで電卓叩いて計算してましたが、そのままでは埒が明かず、どうしようかと思っていたら、HP社のHP67とプリンタ付きのHP97を入社1か月目と2か月目に関周社長が米国出張で買ってきてくれました。朝出社すると机の上に置いてある、うれしかった。秘書に尋ねると「社長がebisuさんに使えって置いてきました」。当時11万円と22万円もした高額の科学技術用プログラマブル計算機でした。一日中計算に明け暮れていたのが、プログラムを組んでしまうとデータ入力とチェックだけでいいので30分で終わってしまったのは感激でした。時間が短縮できるので統計計算量が数倍に増えました。線形回帰分析をベースに、経営分析用の25ゲージのレーダ・チャートを開発しました。組んだプログラムはテストデータでチェック済みですから、計算の確認がいらない。プロジェクト5つ抱えていても問題がなくなりました。収益構造を変えることを目標にシステム化(為替管理、円定価表システム、納期管理システム、仕入在庫管理など)をいくつかやったので、3年後には会社の売上高経常利益率が7%ほどアップしてました。これらのシステムは円定価見積レート、仕入レート、決済レートで連動していました。仕入れと営業実務が劇的に変わりました。
400頁の英文のマニュアル2冊を1週間で読み切り統計関係の数値プログラミングをマスターし、その後2年間の間にさらに2言語プログラミング言語をマスターして仕事で使いました。3年目には会計情報統合システム分野では国内トップレベルのSEと互角に仕事してました。5年目には為替管理や簿記や原価計算、経営分析、在庫管理、初等統計学などの専門知識がある分だけこちらが有利、国内トップレベルのSEを超えましたね。その都度一緒に仕事するソフトハウス(オービック⇒日本電気情報サービス⇒NCD社)は代わりましたが、スキルが上がるとSEたちは何でも言うこと聞いてくれました。8か月で臨床検査最大手SRLの会計情報統合システムが本稼働した後、「暇だからプログラミングやろうかな」って言ったら、「内部設計やプログラミングはわたしたちがやるので、ebisuさんは実務デザインと仕様書書いてください」って。(笑)
コンピュータを扱えることはあたりまえ、それ以外の専門知識が大事。国語と数学と英語の勉強をちゃんとやっておけば、コンピュータ関係の専門書は必要な時に独力で読めるし、仕事で使えばスキルも短期間で飛躍的に伸びます。だから高校生のときには国語と数学と英語の勉強をしっかりやっておこう。大学では専門分野を極めよう。簡単なプログラミングはとっくにブラックの世界ですよ。雇用の安定しない非正規・低賃金です。ゲームソフトの世界も恐らく同じでしょうよ。どうか高校生の皆さんは高額報酬分野を目指して勉強してください。それには国語と数学と英語が大事です。情報の勉強なんか社会人になってからでも独学でやれます。仕事でつかえる環境があればスキルはぐんぐん伸びます。スキルの高いSEと仕事する機会があれば、技術は盗めます。一緒に仕事して見ただけでわかるんです。
さて、高校数学の勉強の話に戻りましょう。ふだんやっている問題集に良問には「良」のマークを付け、できなかった問題には「レ点」をつけてあれば、効率的に復習できます。マークを付けた問題でも2度目にやって十分理解したら、マークに二重線を引いておけば、3度目はパスできます。こうして問題の分量を減らしていけば数分の一の時間で復習できまります。時間は一日24時間しかないから、いかに効率的に復習するかが3年次の学習効果を決定します。ふだんの勉強方式は予習方式です。これが一番効率がいい。なぜかって?習っていないところを予習してあると、どこがわからないかがはっきりしますから、学校の授業は分からなかったところに集中して聴けばいい、つまり復習になってしまうからです。そういう勉強の仕方が学力アップの効率が高い。
<余談:転職≒天職>
1978年の大学新卒の初任給は105,500円でした。産業用エレクトロニクス輸入専門商社の関周社長が入社早々に買ってくれたHP97は22万円ですからずいぶん高い製品だったのです。
本社は日本橋人形町、大学院卒の中途入社でした、初任給は2.5倍ほどいただいたのではなかったか。仕事は期待に応えたと思います。五年後にこの会社を辞めて、職探しにリクルート社の人材斡旋で選んだうちにフェアチャイルドジャパンがありました、経理課長職で年収850万円でした。当時の大卒初任給は135,800円ですから、年収220万円程度です。外資の半導体製造企業は日本企業に勝てそうもないのでいずれ撤退になると判断。プレジデント社とスキルの高い上場準備要員を募集していた臨床最大手SRLに絞って、5年分の決算情報をみて、両方の会社を訪問しました。プレジデント社は赤坂に事務所がありました、雑誌の編集の仕事です、経営や経済記事が中心の雑誌ですから向いていたかもしれません。
上場準備中のSRLはシステム開発の高度なスキルが生かせます。担当できる社員がいなくて困ってました。SRLは西新宿の超高層ビル22階が本社、いまでこそ都庁の手前ですが、当時は都庁は丸の内で西新宿にはまだ移転してません。ビルと業績でSRLに決めました。高校卒業して根室から出て行って、都会で仕事ですから、超高層ビルで一度仕事してみたかった、それだけ。(笑)
その後、横浜の療養型病院の常務理事となり、病棟建て替えをやり終え、また転職。外食産業の別の会社で経営企画次長として銀座3丁目でも仕事することになります。
根室へ戻って来てから、東北の会社からお誘いが一度ありましたが、いくらなんでももう転職はナシです。体力がありません、そのうちにふるさとの土になります。(笑)
https://nenji-toukei.com/n/kiji/10021)
にほんブログ村
#4175 ようやく対数関数に… Feb. 5, 2020 [52. 数学]
根室高校2年生、数学最上位のガンマ1・クラスが先週「対数関数」に入った。2/18(火)から学年末試験が始まるから、微分・積分の章はテスト範囲に含まれないことになるだろう。
クラス編成は次の6段階。
1.ガンマ1
2.ガンマ2
3.ベータ1
4.ベータ2
5.アルファ1
6.アルファ2
クラス編成は次の6段階。
1.ガンマ1
2.ガンマ2
3.ベータ1
4.ベータ2
5.アルファ1
6.アルファ2
数Ⅱはすでに選択科目になっており、「ベーシック数学」を選択履修している生徒もいる。「高校統合」の影響で学力格差が拡大したから、数Ⅱの授業を理解できない生徒がおよそ半数要るのだから、やむを得ない措置だと思う。根室西高校では数Aが2年時の選択科目だったから、およそ半数とみられる成績下位層はそういうレベルに落ちてきている。アルファ・クラスは旧根室西高校生の中の数学が苦手な学力層といって差し支えないだろう。(2年生はガンマとベータ・クラスだけが数Ⅱ履修で、アルファ・クラスは「ベーシック数学」の選択履修組のようだ。)
アルファクラスの生徒は小学校・中学校ですっかり数学アレルギーになった生徒たち。高校普通科の標準的な数学授業を聴いてもチンプンカンプン、だからといって、理解できるところまで勉強しようという意欲の残っている生徒はごく少数。独力では学習できないから、先生の手助けがいる。そういうわけで放課後個別補習が必要になるが、やったところで、数学嫌いになっているので、参加する生徒がほとんどいないと思う。塾へ通うにも、高校生に数学を教えている塾は根室に二つだけ、受け入れられる人数はきわめて限定的である。英語に至っては高校生対象の塾はニムオロ塾ひとつのみ。なかなか難しい教育環境にあるというのが根室の現実。
普通科「特設コース」がガンマ1とガンマ2に分かれている。最上位、ガンマ1クラスの授業進捗がこんなに遅れるのは理由がある。
授業の進捗を他のクラスと同じにしないと、テスト問題の作成に困るし、下位クラスの生徒が努力して上位クラスに食い込むときに、進度が違っていたのでは、授業についていけないという事情がある。最上位のクラスが「微分・積分」の章を終わっており、ガンマ2クラスが対数関数までだと、不都合が起きる。学年末ならほうっておくという選択肢もあるが、前期中間テストや前期期末テスト、後期中間テストでそういう事態が起きたら、実務上困る状況が生まれる。普通科という同じ枠組みで授業をする限り、山登りと同じで、一番遅い人に合わせて登らなければならないのである。標準速度で登れば、普通科の8割の生徒があえなく遭難するだろう。
(γクラスとβ1とβ2クラスは試験問題が一部異なっているようだが、試験範囲は同じである。さらに下のα1とα2クラスがある。学力格差がこれだけ大きい生徒たちを、同じ教科書で教えること自体に無理がある。高校統廃合の失敗例と言ってよい。統廃合検討委員会の面々は、客観的な学力データに基づかぬ議論をしていたということ。委員の委嘱・打診をされても、できもせぬ仕事には首を突っ込むな、この現状を見ろと言いたい。被害者は根室の子どもたちである。)
大学受験を考えたときに、理系学部選択の生徒たちが微分・積分をやっていないというのは、大きなダメージである。学校の授業の進捗には無関係に、受験に間に合うように予習して難易度の高い問題を解いているのは、115人中たった2人の生徒だけ。
学校は、まるで小学生にするように、生徒たちに毎週数学の宿題プリントを課して、やらせている。生徒の自主性や自律性を育てるという目標と、やっていることはまるでちぐはぐ。それでも、そうせざるを得ない、学力低下という事情が背景にあるのだろう。
根室西高校と根室高校を統合してから3年がたつが、この3年間、学力崩壊現象を起こしているように見える。「普通科単位制」の「統合」を道内のほかの地域でやったら、結果は同じことになるだろう。統廃合を主導した道教委の責任も小さくはない。
(統合ではなく、生徒の集まらない高校は「廃校」にすべきなのだろう。そして、合格最低点を公表したらいい。そうすれば、成績の悪い中学生は勉強するよ。「週に5-6日間部活三昧、勉強せず」、なんて生徒はいなくなります。文武両道、普通科で勉強したければ300点満点の五科目合計点で120点、商業科なら90点はどうだろう?15年前には、定員オーバーで普通科の合格最低点が150点を超えた年度もあった。)
こういう環境の中で、大学進学を目指す生徒は、強靭な精神と不屈の向学心をもって挑まなければならないのだろう。その次に位置している学力層の生徒たちがいる。そういう数人の生徒たちと2番手の学力層の生徒たちと教科担当の先生たちとの間に「何か新しい連携」が生まれたら、この数年間、絶対数も進学先の大学の入試難易度も低下し続けているが、大学進学実績を変えられるのではないか。
アルファクラスの生徒は小学校・中学校ですっかり数学アレルギーになった生徒たち。高校普通科の標準的な数学授業を聴いてもチンプンカンプン、だからといって、理解できるところまで勉強しようという意欲の残っている生徒はごく少数。独力では学習できないから、先生の手助けがいる。そういうわけで放課後個別補習が必要になるが、やったところで、数学嫌いになっているので、参加する生徒がほとんどいないと思う。塾へ通うにも、高校生に数学を教えている塾は根室に二つだけ、受け入れられる人数はきわめて限定的である。英語に至っては高校生対象の塾はニムオロ塾ひとつのみ。なかなか難しい教育環境にあるというのが根室の現実。
普通科「特設コース」がガンマ1とガンマ2に分かれている。最上位、ガンマ1クラスの授業進捗がこんなに遅れるのは理由がある。
授業の進捗を他のクラスと同じにしないと、テスト問題の作成に困るし、下位クラスの生徒が努力して上位クラスに食い込むときに、進度が違っていたのでは、授業についていけないという事情がある。最上位のクラスが「微分・積分」の章を終わっており、ガンマ2クラスが対数関数までだと、不都合が起きる。学年末ならほうっておくという選択肢もあるが、前期中間テストや前期期末テスト、後期中間テストでそういう事態が起きたら、実務上困る状況が生まれる。普通科という同じ枠組みで授業をする限り、山登りと同じで、一番遅い人に合わせて登らなければならないのである。標準速度で登れば、普通科の8割の生徒があえなく遭難するだろう。
(γクラスとβ1とβ2クラスは試験問題が一部異なっているようだが、試験範囲は同じである。さらに下のα1とα2クラスがある。学力格差がこれだけ大きい生徒たちを、同じ教科書で教えること自体に無理がある。高校統廃合の失敗例と言ってよい。統廃合検討委員会の面々は、客観的な学力データに基づかぬ議論をしていたということ。委員の委嘱・打診をされても、できもせぬ仕事には首を突っ込むな、この現状を見ろと言いたい。被害者は根室の子どもたちである。)
大学受験を考えたときに、理系学部選択の生徒たちが微分・積分をやっていないというのは、大きなダメージである。学校の授業の進捗には無関係に、受験に間に合うように予習して難易度の高い問題を解いているのは、115人中たった2人の生徒だけ。
学校は、まるで小学生にするように、生徒たちに毎週数学の宿題プリントを課して、やらせている。生徒の自主性や自律性を育てるという目標と、やっていることはまるでちぐはぐ。それでも、そうせざるを得ない、学力低下という事情が背景にあるのだろう。
根室西高校と根室高校を統合してから3年がたつが、この3年間、学力崩壊現象を起こしているように見える。「普通科単位制」の「統合」を道内のほかの地域でやったら、結果は同じことになるだろう。統廃合を主導した道教委の責任も小さくはない。
(統合ではなく、生徒の集まらない高校は「廃校」にすべきなのだろう。そして、合格最低点を公表したらいい。そうすれば、成績の悪い中学生は勉強するよ。「週に5-6日間部活三昧、勉強せず」、なんて生徒はいなくなります。文武両道、普通科で勉強したければ300点満点の五科目合計点で120点、商業科なら90点はどうだろう?15年前には、定員オーバーで普通科の合格最低点が150点を超えた年度もあった。)
こういう環境の中で、大学進学を目指す生徒は、強靭な精神と不屈の向学心をもって挑まなければならないのだろう。その次に位置している学力層の生徒たちがいる。そういう数人の生徒たちと2番手の学力層の生徒たちと教科担当の先生たちとの間に「何か新しい連携」が生まれたら、この数年間、絶対数も進学先の大学の入試難易度も低下し続けているが、大学進学実績を変えられるのではないか。
*#4168 根室高校進路実績H27-30年度比較 Jan. 16, 2016
https://nimuorojyuku.blog.ss-blog.jp/2020-01-16
わたしは、学科編成をこのままにする限りは、割り切るしかないと思う。入試得点で振り分けたら、年度の途中でガンマ1クラスの入れ替えはなし、12月末までに全部の章を終わるスケジュールで授業をする。
教育こそが根室の未来の礎である。根室の教育関係者はもっと教育に関心をもつべきではないか。高校の進路実績データ、授業の捗状況、普段のテスト内容、全国模試での根室高校生の位置の変化をデータに基づいて把握しておくべきだ。中学校で実施している学力テストの平均点はひどく低下してしまっているし、得点分布も、上位層が枯渇化現象を起こしていることは、数十回も弊ブログでデータを挙げて紹介して、警鐘を鳴らしてきた。
根室市教委はいまだに、根室市内の中学校の学力テストデータすら見ようとしない。根室の市街化地域の3中学校は、釧路市内と根室管内の中学校の中で最下位グループをなしている。別海中央中学校よりも平均点が毎回はるかに低いし、中標津の中標津中学や広陵中学に比べても低い。
根室市教委と根室市議会文教厚生常任委員会は、データに基づく議論をされたら如何?チコちゃんに叱られます、「ぼーっとしてんじゃねえよ!」ってね。(笑)
根室で生まれて育つことが、大学進学するときに大きなハンディになってはならぬ。これは根室に住む大人たちの責任だよ。とくに教育関係者の責任が重大であることは論を俟たない。数値目標設定して、ちゃんと仕事しよう。
*#4099 学力テスト総合A18校科目別データ Oct. 11, 2019
https://nimuorojyuku.blog.ss-blog.jp/2019-10-11
<余談:クラス編成替えについて>
仮に中学校の学力テストで60%以上の得点層がギリギリで標準的な普通科の数学授業を理解できるとしたら、11月7日の学力テスト総合Cデータで判断すると、柏陵中学校が66名中8名、啓雲中学校が46名中5名である。合計すると112名中13人ということになる。根室高校への出願は176名(普通科114名、商業科43名、事務情報科19名)だから、そのうちの12%とすると20名だということ。
数学の得点が26点以上の層が2校で25人(22.3%)だから、出願した176名(定員200名)のうち40名しかいない。ほぼ普通科特設コース・クラスの人数と一致している。
だから、普通科特設コースの35人のうちの20名ほどが中学時代に数学の学力テストで60%超の成績であるといえそうだ。ガンマ1クラスだけしか、標準的な難易度の教科書で、1月20日ころまでに教科書全章を終える学力がないということ。
ガンマ1クラスは入学当初の成績でメンバーを固定し、2年当初に行うクラス編成替えは年度末までの成績でやればいい。ふだんの定期テストは学力に応じて問題を別にできる。クラス分けの基礎データは7月と11月と1月に行っている全国模試の合計点数を利用したらいい。
2006年のころの根室高校普通科1年生は、数Ⅰ&Aの授業は1月20日までに終了し、21日から数Ⅱをやっていた。いま、1年生が教科書を終わるのは学年末テストギリギリのはず。明日、生徒に訊いてみよう。1か月遅れている。普通科の生徒の学力格差が大きすぎて、進度を一番学力の低いクラスに合わせるからだろう。やはり、学力データを無視した、無理な統合案だったと言わざるを得ない。道教委主導の「単位制普通科への移行案」に対抗する選択肢が考えつかなかったのだろうと思う。市長の諮問委員会方式というのが諸悪の根源、オープンな場で衆知を集めて議論すべきではないのか?
https://nimuorojyuku.blog.ss-blog.jp/2020-01-16
わたしは、学科編成をこのままにする限りは、割り切るしかないと思う。入試得点で振り分けたら、年度の途中でガンマ1クラスの入れ替えはなし、12月末までに全部の章を終わるスケジュールで授業をする。
教育こそが根室の未来の礎である。根室の教育関係者はもっと教育に関心をもつべきではないか。高校の進路実績データ、授業の捗状況、普段のテスト内容、全国模試での根室高校生の位置の変化をデータに基づいて把握しておくべきだ。中学校で実施している学力テストの平均点はひどく低下してしまっているし、得点分布も、上位層が枯渇化現象を起こしていることは、数十回も弊ブログでデータを挙げて紹介して、警鐘を鳴らしてきた。
根室市教委はいまだに、根室市内の中学校の学力テストデータすら見ようとしない。根室の市街化地域の3中学校は、釧路市内と根室管内の中学校の中で最下位グループをなしている。別海中央中学校よりも平均点が毎回はるかに低いし、中標津の中標津中学や広陵中学に比べても低い。
根室市教委と根室市議会文教厚生常任委員会は、データに基づく議論をされたら如何?チコちゃんに叱られます、「ぼーっとしてんじゃねえよ!」ってね。(笑)
根室で生まれて育つことが、大学進学するときに大きなハンディになってはならぬ。これは根室に住む大人たちの責任だよ。とくに教育関係者の責任が重大であることは論を俟たない。数値目標設定して、ちゃんと仕事しよう。
*#4099 学力テスト総合A18校科目別データ Oct. 11, 2019
https://nimuorojyuku.blog.ss-blog.jp/2019-10-11
<余談:クラス編成替えについて>
仮に中学校の学力テストで60%以上の得点層がギリギリで標準的な普通科の数学授業を理解できるとしたら、11月7日の学力テスト総合Cデータで判断すると、柏陵中学校が66名中8名、啓雲中学校が46名中5名である。合計すると112名中13人ということになる。根室高校への出願は176名(普通科114名、商業科43名、事務情報科19名)だから、そのうちの12%とすると20名だということ。
数学の得点が26点以上の層が2校で25人(22.3%)だから、出願した176名(定員200名)のうち40名しかいない。ほぼ普通科特設コース・クラスの人数と一致している。
だから、普通科特設コースの35人のうちの20名ほどが中学時代に数学の学力テストで60%超の成績であるといえそうだ。ガンマ1クラスだけしか、標準的な難易度の教科書で、1月20日ころまでに教科書全章を終える学力がないということ。
ガンマ1クラスは入学当初の成績でメンバーを固定し、2年当初に行うクラス編成替えは年度末までの成績でやればいい。ふだんの定期テストは学力に応じて問題を別にできる。クラス分けの基礎データは7月と11月と1月に行っている全国模試の合計点数を利用したらいい。
2006年のころの根室高校普通科1年生は、数Ⅰ&Aの授業は1月20日までに終了し、21日から数Ⅱをやっていた。いま、1年生が教科書を終わるのは学年末テストギリギリのはず。明日、生徒に訊いてみよう。1か月遅れている。普通科の生徒の学力格差が大きすぎて、進度を一番学力の低いクラスに合わせるからだろう。やはり、学力データを無視した、無理な統合案だったと言わざるを得ない。道教委主導の「単位制普通科への移行案」に対抗する選択肢が考えつかなかったのだろうと思う。市長の諮問委員会方式というのが諸悪の根源、オープンな場で衆知を集めて議論すべきではないのか?
#4001 「正負の計算」ドリルの珍妙な計算方式 May 21, 2019 [52. 数学]
昨日、中1の生徒が「正負の計算」のプリントをやっていた。見たら計算が違う。根室市で作成・配布したプリント問題だった。
ブロックが互い違いに積み重なっており、生徒は最下段の2項の上部にあるブロックに直下の段の数値を加算して記入していた。「5-2=3」で3を2段目に記入、次に「-2-3=-5」を2段目に記入。次いで2段目の「3-5=-2」を3段目に記入していた。つまり、「5-2-3=」という問題の計算の仕組みをブロックを積み重ねることで表現したかったのだろう。生徒はそのように理解して記入していた。このような計算(2項、3項、4項の加算)のブロック図が並んでいた。正負の数の基礎的計算規則に習熟する大事なところである。
2項の加算の加算の場合は問題が生じないが、3項の計算の場合はこの例のように2回計算される項が生じるから、正しい計算結果にならない。このプリントを作成した人は、どういう意図をブロック図に込めたのだろう。
生徒にはこのプリントの計算方式は正しくないのでやらなくていいと伝えた。学校の先生からなぜやらないのか問われたら、わたしが言ったままを伝えるように頼んだ。
根室市教委は『カルク』という計算問題集を6年前に根室市内の全中学校へ配布したが、校正がなされていなかったのか、解答ミスがたくさんあり、釧路の教育を考える会のメンバーが根室市教委へ指摘して、解答の作成しなおしをしたことがある。学力テストの結果から、根室の中学生の基礎計算力が著しく弱いということが分かっていたので、基礎計算問題集という発想はよかったが、仕事は杜撰だった。
生徒に確認したら修正版がいまも配布されているが、市街化地域の3中学校で授業や宿題に使っている学校はないようだ。大きなチョンボをやると現場の先生たちの信頼がなくなるということだろう。
今回とりあげたプリントがどのような手順でつくられたのかまったく分からないが、チェックがなされていないずさんな仕事になった。6年前と同じことが繰り返されている。
数学担当の先生がこのようなプリントを作成するわけはないと思うが、もし依頼したのならこんな不慣れな作業で現場の先生たちに負荷を掛けてはいけない、低学力の生徒のための放課後補習の時間が奪われる。どうしてもやるなら根室市教委がチェックの手を抜かないことだ。自分たちでそういう仕事ができないことを前回知ったはずと思っていたが、そうではなかったらしい。
このプリントだけはどう考えても数学の先生がつくったものとは思えぬ。誰が指示して誰に作らせ、誰がチェックしたのか、検証作業をして、今後はこのようなことのないように具体的な対策をとってもらいたい。
市販教材を買えばいいだけで、このような杜撰な問題プリントの作成配布は根室の中学生を混乱させ、意図に反して学力低下に寄与してしまう。
四月に実施された中3学力テストの数学の平均点はB中学校が15.2点、C中学校は16.2点である。60点満点のテストで平均点が30%に届いていない、昨年よりもさらに数学の学力低下が進んでいる。釧路市内の14校の昨年の学力テストのデータをモニターしていたがこんなに低い平均点の学校はない。
地域経済の20年後、30年後は現在の小中高生が支えることになることを考えたら、このような学力低下は断じて許容できないはず。根室の地元経営者たちは危機感をもって教育問題を語れ。
根室市議会文教厚生委員会メンバーは市教委が作成配布しているものをチェックすべきだろう。根室市教委任せにしていたら、学力低下に拍車がかかる。足元がお留守になっているのではないか。
*
#2262 計算問題集『カルク』配布(1)
http://nimuorojyuku.blog.so-net.ne.jp/2013-04-14
#2265 『カルク』はすぐれもの(2) : "a good job"
http://nimuorojyuku.blog.so-net.ne.jp/2013-04-16
#2266 『カルク』改善への視点(3)
http://nimuorojyuku.blog.so-net.ne.jp/2013-04-17
#2276 時代錯誤の主張 北海道新聞社説「序列化の懸念拭えない」 Apr. 27, 2013
http://nimuorojyuku.blog.so-net.ne.jp/2013-04-28
#2306 B中学校のみ『カルク』が配布されていないのはなぜ? May 23, 2013
http://nimuorojyuku.blog.so-net.ne.jp/2013-05-23
#2315 B中学校が基礎計算問題集『カルク』を配布 May 31, 2013
https://nimuorojyuku.blog.so-net.ne.jp/2013-05-31-1

にほんブログ村
| -2 | ||||||
| 3 | -5 | |||||
| 5 | -2 | -3 |
ブロックが互い違いに積み重なっており、生徒は最下段の2項の上部にあるブロックに直下の段の数値を加算して記入していた。「5-2=3」で3を2段目に記入、次に「-2-3=-5」を2段目に記入。次いで2段目の「3-5=-2」を3段目に記入していた。つまり、「5-2-3=」という問題の計算の仕組みをブロックを積み重ねることで表現したかったのだろう。生徒はそのように理解して記入していた。このような計算(2項、3項、4項の加算)のブロック図が並んでいた。正負の数の基礎的計算規則に習熟する大事なところである。
2項の加算の加算の場合は問題が生じないが、3項の計算の場合はこの例のように2回計算される項が生じるから、正しい計算結果にならない。このプリントを作成した人は、どういう意図をブロック図に込めたのだろう。
生徒にはこのプリントの計算方式は正しくないのでやらなくていいと伝えた。学校の先生からなぜやらないのか問われたら、わたしが言ったままを伝えるように頼んだ。
根室市教委は『カルク』という計算問題集を6年前に根室市内の全中学校へ配布したが、校正がなされていなかったのか、解答ミスがたくさんあり、釧路の教育を考える会のメンバーが根室市教委へ指摘して、解答の作成しなおしをしたことがある。学力テストの結果から、根室の中学生の基礎計算力が著しく弱いということが分かっていたので、基礎計算問題集という発想はよかったが、仕事は杜撰だった。
生徒に確認したら修正版がいまも配布されているが、市街化地域の3中学校で授業や宿題に使っている学校はないようだ。大きなチョンボをやると現場の先生たちの信頼がなくなるということだろう。
今回とりあげたプリントがどのような手順でつくられたのかまったく分からないが、チェックがなされていないずさんな仕事になった。6年前と同じことが繰り返されている。
数学担当の先生がこのようなプリントを作成するわけはないと思うが、もし依頼したのならこんな不慣れな作業で現場の先生たちに負荷を掛けてはいけない、低学力の生徒のための放課後補習の時間が奪われる。どうしてもやるなら根室市教委がチェックの手を抜かないことだ。自分たちでそういう仕事ができないことを前回知ったはずと思っていたが、そうではなかったらしい。
このプリントだけはどう考えても数学の先生がつくったものとは思えぬ。誰が指示して誰に作らせ、誰がチェックしたのか、検証作業をして、今後はこのようなことのないように具体的な対策をとってもらいたい。
市販教材を買えばいいだけで、このような杜撰な問題プリントの作成配布は根室の中学生を混乱させ、意図に反して学力低下に寄与してしまう。
四月に実施された中3学力テストの数学の平均点はB中学校が15.2点、C中学校は16.2点である。60点満点のテストで平均点が30%に届いていない、昨年よりもさらに数学の学力低下が進んでいる。釧路市内の14校の昨年の学力テストのデータをモニターしていたがこんなに低い平均点の学校はない。
地域経済の20年後、30年後は現在の小中高生が支えることになることを考えたら、このような学力低下は断じて許容できないはず。根室の地元経営者たちは危機感をもって教育問題を語れ。
根室市議会文教厚生委員会メンバーは市教委が作成配布しているものをチェックすべきだろう。根室市教委任せにしていたら、学力低下に拍車がかかる。足元がお留守になっているのではないか。
*
#2262 計算問題集『カルク』配布(1)
http://nimuorojyuku.blog.so-net.ne.jp/2013-04-14
#2265 『カルク』はすぐれもの(2) : "a good job"
http://nimuorojyuku.blog.so-net.ne.jp/2013-04-16
#2266 『カルク』改善への視点(3)
http://nimuorojyuku.blog.so-net.ne.jp/2013-04-17
#2276 時代錯誤の主張 北海道新聞社説「序列化の懸念拭えない」 Apr. 27, 2013
http://nimuorojyuku.blog.so-net.ne.jp/2013-04-28
#2306 B中学校のみ『カルク』が配布されていないのはなぜ? May 23, 2013
http://nimuorojyuku.blog.so-net.ne.jp/2013-05-23
#2315 B中学校が基礎計算問題集『カルク』を配布 May 31, 2013
https://nimuorojyuku.blog.so-net.ne.jp/2013-05-31-1
にほんブログ村
#3987 数Ⅱ「軌跡の問題」 May 8, 2019 [52. 数学]
毎週水曜日はニムオロ塾が休みだから、のんびり。2時ころロードバイクで15㎞ほど走ってきた。走り出したら小雨がぱらついてきたが、そのまま原野をサイクリング。羽音をけたたましくたてながら飛んで行った鳥は、なんだったのだろう。ちっちゃなジェット機が飛んだような音。たまに出くわす。気温13.2度。平均時速21.6km、だいぶ脚に筋力が戻ってきた感じがした。タイヤが細くて、空気圧が8barと高いので雨の路面は要注意だ。まあ、こいうときは走らぬが安全。
『シリウス数Ⅱ』「いろいろな軌跡」p.83に例題が載っている。予習をしていた生徒から質問があったので紹介する。ほとんどの生徒が疑問に思うだろう、いい質問だった。
--------------------------------------------------
<例題>
点(a, b)が円x^2+y^2=1上を動くとき、点(a+b, ab)の軌跡を求めよ。
<解答>
a+b=x、ab=yとおく。
点(a, b)は円x^2+y^2=1上の点であるから、
a^2+b^2=1
a^2+b^2=(a+b)^2-2ab=x^2-2yであるから、
x^2-2y=1
y=(1/2)x^2-1/2…①
a, b は t に関する2次方程式 t^2-xt+y=0 の実数解であるから、判別式をDとすると、
D=x^2-4y≧0
これに①を代入すると、
X^2-4((1/2)x^2-1/2) ≧0
これを解いて、
-√2≦x≦√2
よって、求める軌跡は、
放物線 y=(1/2)x^2-1/2 の -√2≦x≦√2 の部分である。
------------------------------------------------------
生徒から質問のあったのは青字の部分である、なぜ、唐突にこの式がでてくるのか由来がわからないということだった。
(この生徒は塾用数学問題集『シリウス』シリーズを中1から使用して、予習方式で勉強しているが、例題で質問がでたのは記憶にないからおそらくこれが初めて。例題を独力で読み、すんなり理解して難易度の高い問題にただちにチャレンジしてきた。このシリーズは問題の難易度が高いだけでなく、数が多い。問題集は283頁、解答集は557頁、B5版ノートよりも幅と高さがそれぞれ5㎜ほど長い。
高校受験数学で夙(つと)に有名な「青チャート」はほとんどのページが例題で埋め尽くされ、問題は一つの例題につき数題しかないが、問題数の数でいうとシリウス数Ⅱは青チャートの20倍は尤(ゆう)にあるだろう。そして難易度は赤チャートレベル。それを基礎問題集をやらずに、いきなりやり続けて来たのだから、数学の力は高校へ入学してから抜群に伸びた。生活時間の使い方が変わったことが大きい。土日に長時間・集中的に勉強するようになった。中学時代は土日はほとんど勉強していないようすだった。舐めていたのである。根室に居たらこれはもうしかたがない。どれだけ言ったって、高校2年になるまでわからない。(笑)
だれもがこんな学び方ができるわけではない。北海道の公立中学で採用している学力テストは東京都のそれに比べて難易度が低いが、そのテストで満点を取ったことのある生徒でも、こういうやり方をしたのは初めてである。生徒の学力、チャレンジ精神の有無、そして性格に応じて教材とやり方を選べる、個別指導の利点だろう。)
2次方程式の基本に帰れば気がついただろう。軌跡のところで突然にどこから出てきたのかわからない式が提示されたので戸惑ったのだ。2次方程式の実数解は判別式D≧0を満たすことが要件である。それとa,bが実数解だということの2条件を考えたら、解説文の意図するところが理解できる。
『シリウス数Ⅱ』「いろいろな軌跡」p.83に例題が載っている。予習をしていた生徒から質問があったので紹介する。ほとんどの生徒が疑問に思うだろう、いい質問だった。
--------------------------------------------------
<例題>
点(a, b)が円x^2+y^2=1上を動くとき、点(a+b, ab)の軌跡を求めよ。
<解答>
a+b=x、ab=yとおく。
点(a, b)は円x^2+y^2=1上の点であるから、
a^2+b^2=1
a^2+b^2=(a+b)^2-2ab=x^2-2yであるから、
x^2-2y=1
y=(1/2)x^2-1/2…①
a, b は t に関する2次方程式 t^2-xt+y=0 の実数解であるから、判別式をDとすると、
D=x^2-4y≧0
これに①を代入すると、
X^2-4((1/2)x^2-1/2) ≧0
これを解いて、
-√2≦x≦√2
よって、求める軌跡は、
放物線 y=(1/2)x^2-1/2 の -√2≦x≦√2 の部分である。
------------------------------------------------------
生徒から質問のあったのは青字の部分である、なぜ、唐突にこの式がでてくるのか由来がわからないということだった。
(この生徒は塾用数学問題集『シリウス』シリーズを中1から使用して、予習方式で勉強しているが、例題で質問がでたのは記憶にないからおそらくこれが初めて。例題を独力で読み、すんなり理解して難易度の高い問題にただちにチャレンジしてきた。このシリーズは問題の難易度が高いだけでなく、数が多い。問題集は283頁、解答集は557頁、B5版ノートよりも幅と高さがそれぞれ5㎜ほど長い。
高校受験数学で夙(つと)に有名な「青チャート」はほとんどのページが例題で埋め尽くされ、問題は一つの例題につき数題しかないが、問題数の数でいうとシリウス数Ⅱは青チャートの20倍は尤(ゆう)にあるだろう。そして難易度は赤チャートレベル。それを基礎問題集をやらずに、いきなりやり続けて来たのだから、数学の力は高校へ入学してから抜群に伸びた。生活時間の使い方が変わったことが大きい。土日に長時間・集中的に勉強するようになった。中学時代は土日はほとんど勉強していないようすだった。舐めていたのである。根室に居たらこれはもうしかたがない。どれだけ言ったって、高校2年になるまでわからない。(笑)
だれもがこんな学び方ができるわけではない。北海道の公立中学で採用している学力テストは東京都のそれに比べて難易度が低いが、そのテストで満点を取ったことのある生徒でも、こういうやり方をしたのは初めてである。生徒の学力、チャレンジ精神の有無、そして性格に応じて教材とやり方を選べる、個別指導の利点だろう。)
2次方程式の基本に帰れば気がついただろう。軌跡のところで突然にどこから出てきたのかわからない式が提示されたので戸惑ったのだ。2次方程式の実数解は判別式D≧0を満たすことが要件である。それとa,bが実数解だということの2条件を考えたら、解説文の意図するところが理解できる。
(t-a)(t-b)=0
これが、a,bを解とする2次方程式で、a,bが実数であるためには、この方程式の判別式D≧0であればよい。
そこで、これを展開してみる。
t^2 - (a+b)t + ab=0
さて、ここで、
x=a+b, y=ab であったことを思い出してもらいたい。置き換えると、
t^2 -xt +y=0
こういうことだったのである。例題には説明なしにいきなり最後の式がでてきたのだが、全部書くとこのように長くなるので、端折ったのだろう。
「迷ったときには基本に還る」
高校2年生で、いまの時期(5月)に、この例題を予習して、読み切れる生徒はほとんどいないだろう、いい質問だった。
この生徒は中1のときから予習方式で学習しているから、少ない例題を読みこなし、すぐに難易度の高い問題を解くのにすっかり慣れてしまった。高校数学の範囲ならもう独力でぜんぶやれるだろう。数学は塾で教える必要がほとんどなくなっている、それでいい。(笑) 塾の指導目標はそこに置いている。独力でかなりの難易度の問題集を解いたり、独力で参考書を読む力をつけることに目標を置き、そのターゲットを達成するために具体的な指導のやり方を生徒の学力に応じて考えて教えている。音読トレーニングもこの生徒に合わせて選んだ15冊をやり切った、著者の主張の要点析出や批判もしてきた。最後に一緒に読んだのは福沢諭吉『福翁自伝』の前半百ページくらいまでだった。残りは独力で読ませた。いつまでも指導していてよいわけがない。濃密な指導をしすぎて依頼心を生んではいけない。そのあとは独力で物理学者山本義隆著『近代日本150年』岩波新書の読破にチャレンジした。この本はじつに難易度の高い本である。著者は知の職人というにふさわしい。厳密な学術論文を書くスタイルで書き通している。東大大学院で身につけた技術だろう。彼はかつて東大全共闘議長であったことがある。1960年代後半に、湯川博士をして「日本人でノーベル物理学賞に一番近い学生」と言わしめた。その後、山本は東大を去る。東大院生のときに全共闘議長として担がれなければ、東大物理学の名教授として君臨しただろう。人の運命は計り知れぬ。そのお陰で、いい本を何冊も書いている。
塾の音読トレーニングは山本義隆の本で卒業である。あとは興味のわいた本を自分で選んで読めばいい。すでに論理的な文章読解力は並の高校生の比ではない。
ふつうは、教科書レベルからやって、基本問題集を1冊消化してから、シリウスのような難易度の高い問題集にチャレンジするのがあたりまえだ。だが、この生徒はいきなりシリウスで大丈夫である。各章の章末には「入試問題研究(応用編)」が載っているが、そこには難関大学の過去問が並んでいる。最近は「入試問題研究(センター試験)」レベルの問題が簡単に感じるというようになった。だから、進研模試の偏差値は80を超えてしまっている。最近は駿台模試、河合塾模試、ゼット会模試の問題に焦点を当てて学習するようになった。とっくに塾で勉強しているだけではない。自分で判断してどういう勉強の仕方が自分に合っているのか、考えながら試行錯誤している。
ひとつ解説し忘れたことを思い出したので補足しておきたい。t についての2次方程式にしているのは、xとyがすでに使ってしまっている文字だから混乱を起こさないための配慮で、他の文字ならなんでもよい。助変数のtとは関係がない。何かの式が背後にあるのではと探しても、説明したような理由で採用した文字だからなにも見つからぬ。そういうことを考えるとsで表したほうがよかったのかもしれない。
さて、この式 t^2-xt+y=0 が思いつかなければ、この問題が解けないかというとそうではない。別の解き方がある。グラフの概形を描けば、簡単にx=(a+b)の定義域がわかる。
Grapsで描いたグラフを見てもらいたい。
(Grapsはフリーソフトだから、ダウンロードして誰でも使えます)
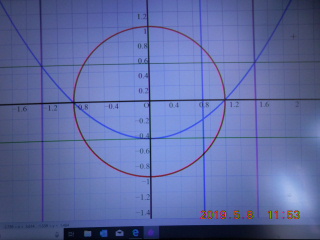
ディスプレイをそのまま写真に撮ったので見づらいだろうが、細かいところはどうでもいいので、半径1の円のグラフと②の放物線に注目していただきたい。
(a+b,ab)の軌跡を求まるのだが、a+bの最小値と最大値は半径1の円を見ただけですぐにわかる。tan45°のところが、a=√2/2であり、b=√2/2であることは簡単に読みとれる。a+b=√2で最大値。
最小値は、tan225°のところ、a=-√2/2、b=-√2/2、a+b=-√2。abの最小値と最大値はもう説明するまでもないだろう。
あとは余談である、EXCELで、0.01刻みで、次のような表を作って、変化をみた。ブログの容量の関係で、途中の行を端折ったが、xは-1.00から+1.00まで0.01刻みで列の数値が計算されている。5ラインしかコピペしていないが、実際には200ラインある。xが-1.00から+1.00まで200段階で他の変数や式が自動計算されて並ぶので、変化の様子が手に取るようにわかる。その大きな表とGRAPSのグラフを突合しながら見れば、理解が深くなる。表からグラフイメージを自分の脳に描いてみよう。そしてGRAPSのグラフと比べてみたらいい。表からグラフをイメージするのに慣れたら、高校数学に抜群に強くなれる。
最上段は変数や計算式である。式が違うが、4番目と5番目の数値が一致するのはどちらも ab を表しているからだ。これはこれで面白い、グラフとは別のところでなるほどと思うところがある。
GRAPSやEXCELを使って遊んでみたらいい。やりかたがわからなかったら、簡単だから教えてあげる。
高校数学まではグラフイメージをあたまに浮かべるとか、グラフ概形を描いてみたら、問題の意図しているところが精確に読み取れる問題が多い。高校数学を卒業して複素関数を学ぶときにはそういう方法が使えなくなる。数学はその辺りから抽象度を一気に上げてしまう。高校数学の覇者たちが、数学科へ進学してつぶれるものが多いのは、複素関数や数理論理学がまったく別のゾーンにあるからだ。
大学生になったら、文系理系を問わず、ユークリッド『原論』に目を通してもらいたい。学の体系構成の要点が理解できる。とくに経済学を学ぶ学生はかならず目を通したほうがいい。理由は「#3938 新しい経済社会のデザインについて」をお読みください。
*https://nimuorojyuku.blog.so-net.ne.jp/2019-02-26
https://nimuorojyuku.blog.so-net.ne.jp/2016-09-06
https://nimuorojyuku.blog.so-net.ne.jp/2011-03-31

にほんブログ村
(Grapsはフリーソフトだから、ダウンロードして誰でも使えます)
ディスプレイをそのまま写真に撮ったので見づらいだろうが、細かいところはどうでもいいので、半径1の円のグラフと②の放物線に注目していただきたい。
(a+b,ab)の軌跡を求まるのだが、a+bの最小値と最大値は半径1の円を見ただけですぐにわかる。tan45°のところが、a=√2/2であり、b=√2/2であることは簡単に読みとれる。a+b=√2で最大値。
最小値は、tan225°のところ、a=-√2/2、b=-√2/2、a+b=-√2。abの最小値と最大値はもう説明するまでもないだろう。
あとは余談である、EXCELで、0.01刻みで、次のような表を作って、変化をみた。ブログの容量の関係で、途中の行を端折ったが、xは-1.00から+1.00まで0.01刻みで列の数値が計算されている。5ラインしかコピペしていないが、実際には200ラインある。xが-1.00から+1.00まで200段階で他の変数や式が自動計算されて並ぶので、変化の様子が手に取るようにわかる。その大きな表とGRAPSのグラフを突合しながら見れば、理解が深くなる。表からグラフイメージを自分の脳に描いてみよう。そしてGRAPSのグラフと比べてみたらいい。表からグラフをイメージするのに慣れたら、高校数学に抜群に強くなれる。
最上段は変数や計算式である。式が違うが、4番目と5番目の数値が一致するのはどちらも ab を表しているからだ。これはこれで面白い、グラフとは別のところでなるほどと思うところがある。
| x | y=(1-x^2)^0.5 | x+y | xy | y=0.5(x+y)^2-0.5 | ||
| -1.00 | 0.0000 | -1.0000 | 0.0000 | 0.0000 | ||
| -0.99 | 0.1411 | -0.8489 | -0.1397 | -0.1397 | ||
| -0.98 | 0.1990 | -0.7810 | -0.1950 | -0.1950 |
| √2/2 | -0.71 | 0.7071 | 0.0000 | -0.5000 | -0.5000 |
| √2/2 | 0.71 | 0.7071 | 1.4142 | 0.5000 | 0.5000 |
GRAPSやEXCELを使って遊んでみたらいい。やりかたがわからなかったら、簡単だから教えてあげる。
高校数学まではグラフイメージをあたまに浮かべるとか、グラフ概形を描いてみたら、問題の意図しているところが精確に読み取れる問題が多い。高校数学を卒業して複素関数を学ぶときにはそういう方法が使えなくなる。数学はその辺りから抽象度を一気に上げてしまう。高校数学の覇者たちが、数学科へ進学してつぶれるものが多いのは、複素関数や数理論理学がまったく別のゾーンにあるからだ。
大学生になったら、文系理系を問わず、ユークリッド『原論』に目を通してもらいたい。学の体系構成の要点が理解できる。とくに経済学を学ぶ学生はかならず目を通したほうがいい。理由は「#3938 新しい経済社会のデザインについて」をお読みください。
*https://nimuorojyuku.blog.so-net.ne.jp/2019-02-26
https://nimuorojyuku.blog.so-net.ne.jp/2016-09-06
https://nimuorojyuku.blog.so-net.ne.jp/2011-03-31
にほんブログ村





