#3897 w=z^(2+i) :複素関数の世界へ Jan. 12. 2019 [52. 数学]
忘年会で釧路へ行ったときに、イオンの熊沢書店を覗くと数学書のコーナーには専門書が10冊ほどあり、そのなかに面白そうな本が2冊ありました。一つは『高校生からわかる複素関数』で9月に出版されたばかりの「出来立てのほやほや」の本、そしてもう一つ興味を引く本『πとeの話』という無限級数に関する本です。興味のある分野の本が2冊並んでいたので、まよわず購入、二つ揃えて並べてくれた店員さんに感謝です。
πやeを無限級数に展開すると三角関数と関係がでてきますが、オイラーの公式はそれらの関係を端的に表現したものです。複素関数にはπとeが必須の道具として登場し、実関数の世界とは別世界の複素解析の世界へとわたしたちを誘(いざな)ってくれます。
オイラーの公式は「e^iΘ=cosΘ+isinΘ」ですが、Θをπに置きなおすとcosπ=1 & sinπ=0ですから、「e^iπ=1」、1を左辺へ移行すると「e^iπ-1=0」、eとπと1と0という基本的な要素のみ、夾雑物ゼロのシンプルな式が出てきます。まざりっけなしですからとっても美しいでしょ、無限級数へ展開すればこれらの関係に気がつく可能性が大きくなりますが、気がついたオイラーは数字の感覚がとってもよかった人なんでしょうね。代表的な無限級数の間にある関係を数字をいじくり合わしているうちに見つけてしまった。複素数の世界では指数関数が三角関数に置き換えられることに気がついた。たぶん、数字遊びをしていただけなのでしょう。数学の世界では誰も目にしたことのない宝物を発見した気分だったはず。
本棚に積んで肥しにするにはもったいないので、正月3日から、暇を見つけては『高校生からわかる複素関数』の例題を一つずつ解いている(笑)のですが、歳のせいかときどきカメさんよりも速度が遅くなります。
95頁に「w=z^(2+i)の振る舞い」という解説があり、「(1)zの実部だけを変化(虚部固定)させたときのw=z^(2+i)の振る舞い」が独立変数のz平面とそれに対応する関数値を表すw平面に分割してグラフが描かれています。複素数は4次元の世界ですからこう(分割)するしかないのです。
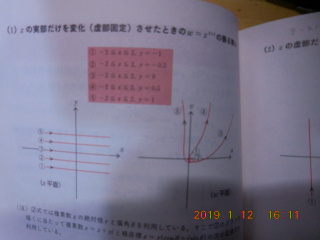
載せられている条件が①~⑤まであります。
①-2≦x≦2、y=-1
②-2≦x≦2、y=-0.5
③-2≦x≦2、y=0
④-2≦x≦2、y=0.5
⑤-2≦x≦2、y=1
たとえば、(-2+i)^2なら高校2年生でも計算できますね。指数部分が整数なら計算は容易、指数部が分数になったら(つまり無理数)たぶん計算があやしくなります。しかし、指数部が複素数になったらまるで話は別で、高校の範囲を完全にはみ出てしまい、次のような計算をすることになります。
w=z^a=e^a(lnr+iΘ0)
この問題の場合は、
w=z^(2+i)=....=e^(2lnr-Θ0)×{cos(lnr+2Θ0)+isin(lnr+2Θ0)
zにターゲットの複素数を変数として代入すれば、関数値が計算できます。実関数とは違って線ではなく、複素平面全体を代入することになるので、グラフの概形を描くだけでも計算量が膨れ上がります。
そのうえネイピア数や自然対数や三角関数がでてきて、計算そのものがやっかいです。複素数の冪(ベキ)関数で繰り返しこの種の計算をしてだいぶトレーニングを積みました。計算は考えなくてもできるところまで習熟するのが肝。いつも生徒に言っていることですが、大事なことだからもちろん自分でもこのようにやってるんです。(笑)
グラフの挙動を確認するために、①をxを0.5ずつ増やした時に計算値がどうなるかやってみました。指数関数や三角関数に展開するのは面倒ですから、手持ちの科学技術計算用の計算機HP-35sには複素数の計算機能があるので利用します。たった11,800円で買えます。日本語と英文マニュアルのついているものを買ってください。EXCELにも複素関数機能があるといいのですが…
1. (-2-i)^(2+i)=-11.7+71.8i
2. (-1.5-i)^(2+i)=-8.1+41.0i
3. (-1.0-i)^(2+i)=-7.2+19.8i
4. (-0.5-i)^(2+i)=-6.6+7.0i
5. (0-i)^(2+i)=-4.8+-0.6i
6. (0.5-i)^(2+i)=-1.9+-3.3i
7. (1.0-i)^(2+i)=1.5-4.1i
8. (1.5-i)^(2+i)=4.9-3.2i
9. (2.0-i)^(2+i)=7.9-1.0i
Z平面の実軸の値が増えるとW平面の実軸も増えていますが、虚軸のほうの値は揺れていますね。Z平面からW平面への対応ですから、面全体が変数となってそれに対応する複雑な形状の面を紡ぎだしているのでしょう。4次元ですからちっともわかりません。①だけでこれだけ計算しなくっちゃなりませんから、①~⑤までやると五倍ですからね。(2)では、実部を固定して虚部を0.5刻みで計算するとやはり45個の計算が必要です。(3)ではZの大きさを固定し、偏角をπ/6ごとに計算すると24個の計算が必要になります。合計114個、ずいぶんたくさんになります。どうやって図を描いたのでしょう?(複素数の計算機能をもったプログラム言語(たとえばC++)でプログラミングするしかなさそうにみえます。*)
これを指数関数と三角関数に展開してやるのではうんざりです。複素数を扱える計算機は、複素数のべき乗関数問題をやるときには便利がいい。
W平面上にプロットしてみたが、滑らかな曲線になっていますから、計算違いはなさそうですが、写真の図に載っている線とはまるで違ってしまいました。
さて、どこで間違えたのでしょう?
計算機の使い方をまちがえたのだろうかと、93頁に載っている問題で操作を確認してみました。
(1+√3 i)^(2+i)
この計算をHP-35sの複素関数機能を利用してやると、-1.317+0.4860.4867iです。
この式を主値をn=0としすると、つぎの計算式で求められます。
4e^-2π/3×{cos(ln2+2π/3)+isin(ln2+2π/3)}
これも計算機でやってみましたが、同じ値がでました、どうやら操作は適正なようです。
(表示は3桁のサイエンスモードにしてあるから、0.4867は「4.867E-1」)
いまは原因がわからない、少し先へ進んでからまた戻ってやってみます、だんだん慣れて理解が進んできます。お酒の醸造をしているようなものです。ときどき惑いすったもんだするのも楽しみの一つ。
ほかのグラフも転載しておきます。
これはzの虚部だけを変化(実部固定)させたときのw=z^(2+i)の振る舞い。
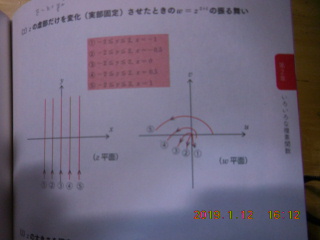
こちらはZの大きさを固定し、偏角を変化させたw-z^(2+i)の振る舞い。

こうして遊んでいるので、ブログの更新頻度が落ちています。複素数という少し広い視野から数学をながめたくなりました。
<余談:C++と複素関数>
複素数は実部と虚部があるので、ダブル型の関数です。ネット検索してみたら、次の命令セットで記述できます。
class complex {
double re, im;
};
グラフ展開するにはまた別のブログラムが必要です。
このオラクルのサイトにC++の複素演算ライブラリーの使用マニュアルが載ってます。
https://docs.oracle.com/cd/E19205-01/820-1213/bkaly/
ふたつのOSに載るコンパイラーが無償提供されています。ひとつはSolarisというUNIX系のOSでもう一つはオープンソースのLINUXです。サンマイクロシステムズが開発して提供(2007年)していましたが、同社がOracle社に買収されて、現在はそこから無償提供されています。C++のコンパイラーもついているようですから、ありがたいですね。97年ころにBorland社のC++コンパイラーが5万円ほどしていましたから、無償提供はありがたい。LINUXをインストールしたマシンを用意すれば使えます。Windows版があるとだれでも使えるのですが、ないかな?
探したらありました。「Visual Studio 2017 Community」というWindows10用のコンパイラーが無償提供されています。いい時代になりましたね。
*https://www.softantenna.com/wp/tips/visual-studio-2017-install/
マイクロソフト社の[visual studio] 無償ダウンロード用公式サイトです。もちろんテキストエディタもついています。
*https://visualstudio.microsoft.com/ja/
** C++の演算子一覧表
https://ja.wikipedia.org/wiki/CとC%2B%2Bの演算子
πやeを無限級数に展開すると三角関数と関係がでてきますが、オイラーの公式はそれらの関係を端的に表現したものです。複素関数にはπとeが必須の道具として登場し、実関数の世界とは別世界の複素解析の世界へとわたしたちを誘(いざな)ってくれます。
オイラーの公式は「e^iΘ=cosΘ+isinΘ」ですが、Θをπに置きなおすとcosπ=1 & sinπ=0ですから、「e^iπ=1」、1を左辺へ移行すると「e^iπ-1=0」、eとπと1と0という基本的な要素のみ、夾雑物ゼロのシンプルな式が出てきます。まざりっけなしですからとっても美しいでしょ、無限級数へ展開すればこれらの関係に気がつく可能性が大きくなりますが、気がついたオイラーは数字の感覚がとってもよかった人なんでしょうね。代表的な無限級数の間にある関係を数字をいじくり合わしているうちに見つけてしまった。複素数の世界では指数関数が三角関数に置き換えられることに気がついた。たぶん、数字遊びをしていただけなのでしょう。数学の世界では誰も目にしたことのない宝物を発見した気分だったはず。
本棚に積んで肥しにするにはもったいないので、正月3日から、暇を見つけては『高校生からわかる複素関数』の例題を一つずつ解いている(笑)のですが、歳のせいかときどきカメさんよりも速度が遅くなります。
95頁に「w=z^(2+i)の振る舞い」という解説があり、「(1)zの実部だけを変化(虚部固定)させたときのw=z^(2+i)の振る舞い」が独立変数のz平面とそれに対応する関数値を表すw平面に分割してグラフが描かれています。複素数は4次元の世界ですからこう(分割)するしかないのです。
載せられている条件が①~⑤まであります。
①-2≦x≦2、y=-1
②-2≦x≦2、y=-0.5
③-2≦x≦2、y=0
④-2≦x≦2、y=0.5
⑤-2≦x≦2、y=1
たとえば、(-2+i)^2なら高校2年生でも計算できますね。指数部分が整数なら計算は容易、指数部が分数になったら(つまり無理数)たぶん計算があやしくなります。しかし、指数部が複素数になったらまるで話は別で、高校の範囲を完全にはみ出てしまい、次のような計算をすることになります。
w=z^a=e^a(lnr+iΘ0)
この問題の場合は、
w=z^(2+i)=....=e^(2lnr-Θ0)×{cos(lnr+2Θ0)+isin(lnr+2Θ0)
zにターゲットの複素数を変数として代入すれば、関数値が計算できます。実関数とは違って線ではなく、複素平面全体を代入することになるので、グラフの概形を描くだけでも計算量が膨れ上がります。
そのうえネイピア数や自然対数や三角関数がでてきて、計算そのものがやっかいです。複素数の冪(ベキ)関数で繰り返しこの種の計算をしてだいぶトレーニングを積みました。計算は考えなくてもできるところまで習熟するのが肝。いつも生徒に言っていることですが、大事なことだからもちろん自分でもこのようにやってるんです。(笑)
グラフの挙動を確認するために、①をxを0.5ずつ増やした時に計算値がどうなるかやってみました。指数関数や三角関数に展開するのは面倒ですから、手持ちの科学技術計算用の計算機HP-35sには複素数の計算機能があるので利用します。たった11,800円で買えます。日本語と英文マニュアルのついているものを買ってください。EXCELにも複素関数機能があるといいのですが…
1. (-2-i)^(2+i)=-11.7+71.8i
2. (-1.5-i)^(2+i)=-8.1+41.0i
3. (-1.0-i)^(2+i)=-7.2+19.8i
4. (-0.5-i)^(2+i)=-6.6+7.0i
5. (0-i)^(2+i)=-4.8+-0.6i
6. (0.5-i)^(2+i)=-1.9+-3.3i
7. (1.0-i)^(2+i)=1.5-4.1i
8. (1.5-i)^(2+i)=4.9-3.2i
9. (2.0-i)^(2+i)=7.9-1.0i
Z平面の実軸の値が増えるとW平面の実軸も増えていますが、虚軸のほうの値は揺れていますね。Z平面からW平面への対応ですから、面全体が変数となってそれに対応する複雑な形状の面を紡ぎだしているのでしょう。4次元ですからちっともわかりません。①だけでこれだけ計算しなくっちゃなりませんから、①~⑤までやると五倍ですからね。(2)では、実部を固定して虚部を0.5刻みで計算するとやはり45個の計算が必要です。(3)ではZの大きさを固定し、偏角をπ/6ごとに計算すると24個の計算が必要になります。合計114個、ずいぶんたくさんになります。どうやって図を描いたのでしょう?(複素数の計算機能をもったプログラム言語(たとえばC++)でプログラミングするしかなさそうにみえます。*)
これを指数関数と三角関数に展開してやるのではうんざりです。複素数を扱える計算機は、複素数のべき乗関数問題をやるときには便利がいい。
W平面上にプロットしてみたが、滑らかな曲線になっていますから、計算違いはなさそうですが、写真の図に載っている線とはまるで違ってしまいました。
さて、どこで間違えたのでしょう?
計算機の使い方をまちがえたのだろうかと、93頁に載っている問題で操作を確認してみました。
(1+√3 i)^(2+i)
この計算をHP-35sの複素関数機能を利用してやると、-1.317+0.4860.4867iです。
この式を主値をn=0としすると、つぎの計算式で求められます。
4e^-2π/3×{cos(ln2+2π/3)+isin(ln2+2π/3)}
これも計算機でやってみましたが、同じ値がでました、どうやら操作は適正なようです。
(表示は3桁のサイエンスモードにしてあるから、0.4867は「4.867E-1」)
いまは原因がわからない、少し先へ進んでからまた戻ってやってみます、だんだん慣れて理解が進んできます。お酒の醸造をしているようなものです。ときどき惑いすったもんだするのも楽しみの一つ。
ほかのグラフも転載しておきます。
これはzの虚部だけを変化(実部固定)させたときのw=z^(2+i)の振る舞い。
こちらはZの大きさを固定し、偏角を変化させたw-z^(2+i)の振る舞い。
こうして遊んでいるので、ブログの更新頻度が落ちています。複素数という少し広い視野から数学をながめたくなりました。
<余談:C++と複素関数>
複素数は実部と虚部があるので、ダブル型の関数です。ネット検索してみたら、次の命令セットで記述できます。
class complex {
double re, im;
};
グラフ展開するにはまた別のブログラムが必要です。
このオラクルのサイトにC++の複素演算ライブラリーの使用マニュアルが載ってます。
https://docs.oracle.com/cd/E19205-01/820-1213/bkaly/
ふたつのOSに載るコンパイラーが無償提供されています。ひとつはSolarisというUNIX系のOSでもう一つはオープンソースのLINUXです。サンマイクロシステムズが開発して提供(2007年)していましたが、同社がOracle社に買収されて、現在はそこから無償提供されています。C++のコンパイラーもついているようですから、ありがたいですね。97年ころにBorland社のC++コンパイラーが5万円ほどしていましたから、無償提供はありがたい。LINUXをインストールしたマシンを用意すれば使えます。Windows版があるとだれでも使えるのですが、ないかな?
探したらありました。「Visual Studio 2017 Community」というWindows10用のコンパイラーが無償提供されています。いい時代になりましたね。
*https://www.softantenna.com/wp/tips/visual-studio-2017-install/
マイクロソフト社の[visual studio] 無償ダウンロード用公式サイトです。もちろんテキストエディタもついています。
*https://visualstudio.microsoft.com/ja/
** C++の演算子一覧表
https://ja.wikipedia.org/wiki/CとC%2B%2Bの演算子
2019-01-12 17:57
nice!(0)
コメント(0)






コメント 0